Diffusion 从入门到入土

Introduction

Creating noise from data is easy; creating data from noise is generative modeling – Songyang

这是一份关于Diffusion model的教程，和市面上很多教程不太一样的是，我会着重从high level的角度介绍如何去从0开始根据一些principle idea来推导出模型的结构，对于过于细节的math可能会一笔带过，因为对我来说这并不是重点。

Diffusion模型可以算是最近几年最为强大的生成模型，无论是理论推导，还是实际工程效果，无不透露出一种特殊的美感，我第一次接触diffusion模型其实并不是从变分框架的角度，而是从随机微分方程(SDE)的角度看待加噪和去噪的过程，这种随机中蕴含的确定性可逆的特性深深吸引了我，也驱使着我探究这份来源于物理学的美。

因为这个领域并没有自顶向下一次性提出一个完整的理论，实际上是由不同的视角逐步探索，最后收敛于同一个框架，用SDE去解释也是2021年才提出的，网上的很多tutorial对这个角度可能都不是很详细，为了记录我的思考过程，这篇blog是以一个自顶向下的SDE视角来解释Diffusion mdel，希望能对你有所帮助:p

SDE

微分方程

在现实的世界中，我们常常寻求变量间变化的直接关系，也就是想找到一种函数来描述变量间的联系，但是有时只能获得变量与变量间接变化的信息，而微分方程描述的就是这样包含导数的信息，微分方程的解就是变量间的直接函数关系。

下面以一阶微分方程举例，一般的形式是

例如：

对于第一个微分方程，我们可以用分离变量的方法求解，但是对于第二个，是无法用初等函数表示解，也就是某种程度上不可解，对于这样不可解的微分方程，我们常用的几何法来绘制出“方向场”，而得到的解为“积分曲线”。

几何法就是在坐标平面上的每一点用“线素”来标示出该点的斜率，而点的斜率值就是。而积分曲线在其曲线的每个点上都和“线素”相切，它也就是微分方程解函数的图像。对于不同的初值，对应会有相应的解。下图以logistic differential equation 示例

这个例子是有解析解的，对应如果我们需要计算时刻的值，只需要

Wiener Process

维纳过程其实就是布朗运动，对于像粒子这种有可能纯粹随机运动的情况，我们需要引入随机性的方程来描述运动规律，比如下图展示了一个粒子在二维空间中的轨迹：

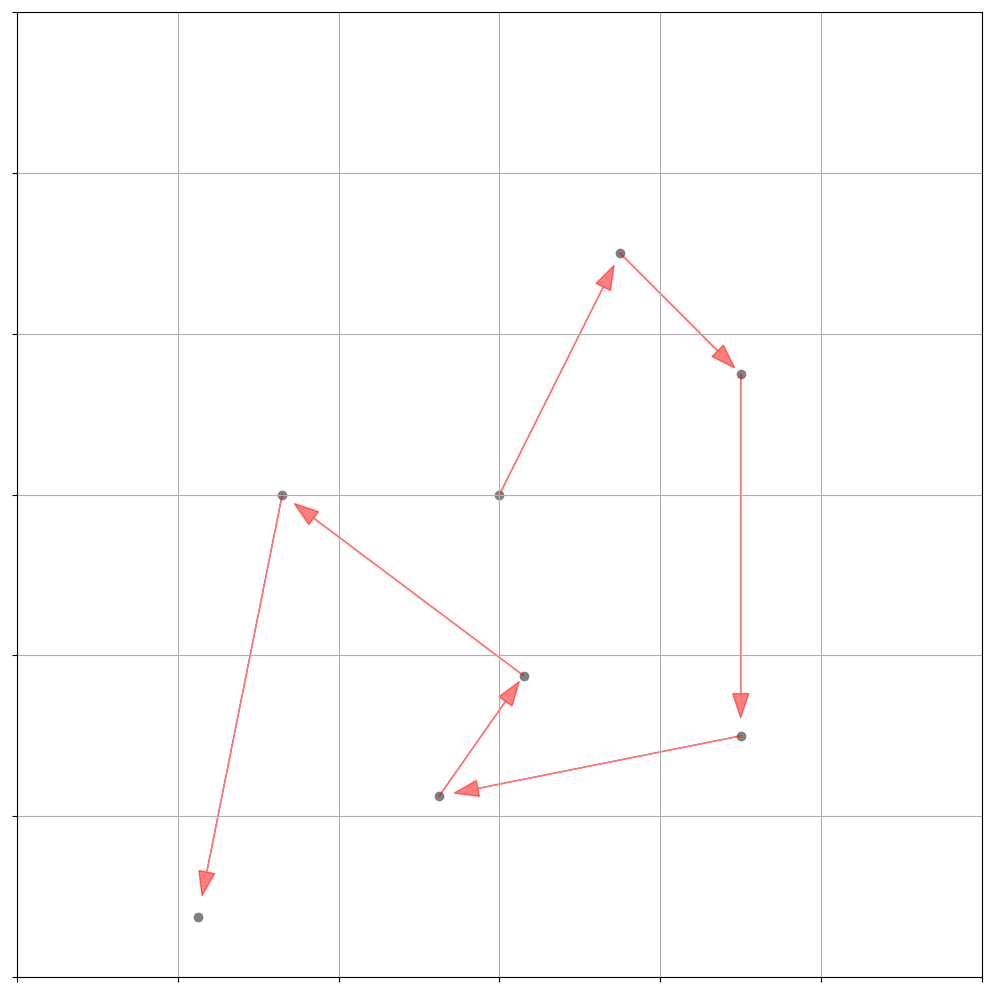
上面的式子描述的一维的简单情况，之间都是独立的，因为对于的采样是和时间不相关的，因为引入了这样的随机变量，也变成了随机变量，其变化由上面的微分方程描述。

出于简单以及高斯良好的性质(convergence of sequences of random variables, nice theoretical properties)，采样自简单的高斯，对于时间变化，这里选择用，目的是方便后续方差相关统计量的推导。

下面来分析一下这个随机变量，不妨设初始位置：

其均值和方差为：

为了符号统一，我们将用规范的来表示，Wiener process主要有三个性质：

Independent increments: 高斯的不相关就是独立, for
Gaussian increments:
Continuous paths in time: 随着时间的movement是连续的，因此当我们无限放大上面图片中的轨迹，不存在不连续的跳变，这是因为Wiener process是随机过程，也就是不可导的

随机微分方程

了解了微分方程和Wiener process后，一个自然的想法就是结合这两者，而这也正是随机微分方程的定义，Ito drift-diffusion processes定义为：

为了示意方便，下面假设constant mean ，以及constant diffusion ：

the Brownian motion is a random variable, which

但是实际上一般的SDE的和是和以及联系的，用于描述他们关系的函数也可能是极为复杂 :p：

Ito’s Lemma

当前所说的SDE描述的是随机变量间的联系，也就是在值域mapping方面建模，但并没有显式地体现出随机变量的另一个维度，也就是概率分布的角度，当我们感兴趣的是随机变量概率分布的演化过程时，就需要对原本的SDE进行变换，最终得到的方程称为Fokker–Planck equation。

下面我会介绍Fokker–Planck equation是怎么推出的，因为概率分布是随机变量的函数，我们感兴趣的是随机变量函数的演化过程，而描述这样关系的SDE微分规则正是非常著名的伊藤引理(Ito’s Lemma)，假设我们有

令，满足二阶可微，那么则有

This is an extremely powerful fact because it says that any (twice differentiable) function of a diffusion is also a diffusion

Fokker–Planck equation

多元函数也是类似的结论，有了Ito’s Lemma这样强大的工具，现在我们知道Fokker–Planck equation其实也应该是个diffusion equation，具体的推导过程如下：

这里是标准布朗运动 (standard Brownian motion)。令为在时的PDF。固定，并定义函数，使其满足，且当，。比如，我们可以选择，其满足当，，并定义。
根据伊藤引理 (Ito’s lemma)，我们有

等式两边同时取期望，我们有

等式两边同时从积分到，由于，我们有

通过分部积分 (integration by parts)，并根据和Fubini定理，我们可以得到

同理，我们计算得到

由于

，且是任意选取的，我们得到

这就是一维Fokker-Planck方程, 又叫一维Kolmogorov前向方程。

对于Winner Process其实就是：

给定初值条件位于，也就是，所得到的解析解为：

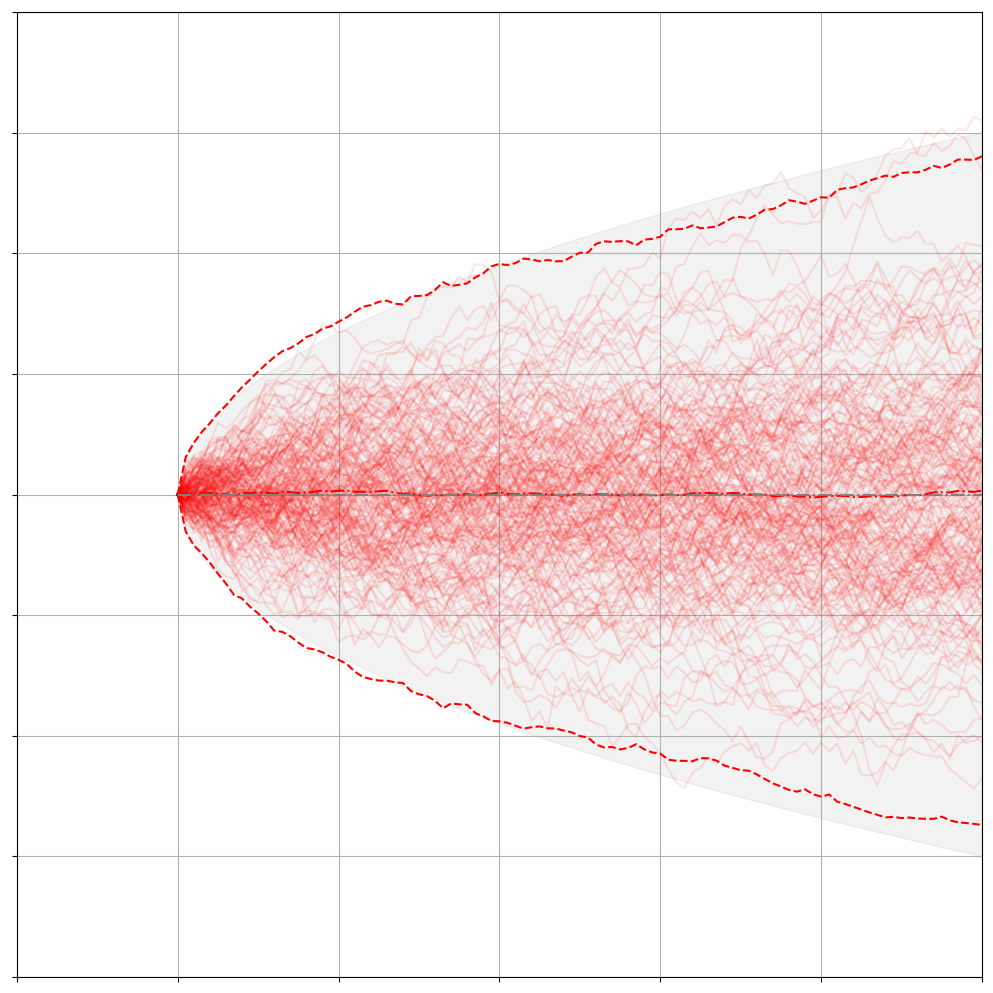
下面描述的就是布朗运动的Fokker-Planck方程与实际采样的结果：

Brownian dynamics simulation for particles in 1-D linear potential compared with the solution of the Fokker–Planck equation

并不是所有的FPE都有解析解，绝大多数的情况还是没有解的，所以人们会重点研究那些特殊的有解方程，Ornstein-Uhlenbeck-like processes 就是其中的一类SDE。

Invertible!

Special Case

在前向过程中不断添加噪声的过程好比是将一杯咖啡加入牛奶，棕色和白色不断扩散，但是如果是反向从一杯拿铁中分离出一杯牛奶和一杯咖啡，多少有一些违反直觉，但是事实是，对于有些前向扩散的SDE，数学上也会很容易定义一个time reverse process governed by a SDE，我们真的可以模拟这个可逆的过程，因为数学毕竟不是物理现实，通过把时间变量取反，我们是可以做到像林克一样使用倒转乾坤 :p。

直观上来看，diffusion process是粒子不断发散的过程，那么这个逆过程一定就是不断聚合粒子，那么有没有一种SDE满足这样的特性，之前小节提到的OU process其实正是这样的过程：

this process compresses a Gaussian until it becomes a delta function centered at x0 at time T

对于最简单的Wiener Process的逆过程，我们可以先利用离散的Euler-Maruyama time steps模拟，其实就是把时间变量取反：

然后写出对应的SDE：

对应Fokker–Planck equation的解为：

为了更直观的理解，我用代码模拟了这个前向和逆向的过程，可以看到逆向最后分布是收敛于delta分布的：

Forward Backward

Gerneral Case

对于一般的1D Diffusion来说：

对应的逆过程SDE应该是：

这里给出构造性证明，同一时刻逆向的分布和前向的分布是一致的，可以得到：

对于前向过程满足

把时间逆转，满足

由于，因此是如下Fokker–Planck equation的解

因此我们构造出了逆过程的SDE，推广到 -dimension，SDE的形式是：

将换元，可以得到：

Magical way to generate samples

不知道在看到了SDE这可以用magical来形容的结果后，你是否和我一样感到兴奋无比，因为这的确提供了一种关于生成过程的新思路，如果拥有超乎寻常的洞察力，以及对于热力学夯实的数学功底，重返2015年，说不定真的可以自己提出Diffusion模型:p，这里我会拿Diffusion作者最初的motivation举例，希望能提供给你一些insights。

当你看到一滴墨水在水中扩散时，你会想到什么，如果给你一张全是noise的图片，你又能发掘出什么。原作者就在墨水扩散的过程中看到了sde的可逆性，并且如果把时间尺度缩小，粒子在微小时间间隔内的forward和backward其实都可以视为布朗运动，对应高斯的diffusion，作者曾经花了大把时间看一副全是noise的图片，从中看到了各种物体，这其实也就是denoise的思想。

让我们反思2015年前的模型，主要分为GAN和VAE两类，基于变分架构的VAE对后验分布很难选择，后续的改进工作很多都是针对这个后验，比如引入normalizing flow来提升变分后验的表达能力，但是GAN和normalizing flow，其实都只是针对生成器建模，这点来说要比VAE更加直接，但是相应的他们也有自己的问题，比如GAN要训练判别器收敛难，normalizing flow的限制太强，表达能力不够，针对于这些问题，我们能否设计出一个新的生成架构，也就是只对生成器建模，不需要后验或者判别器额外建模，也具有强大的表达能力。

而Diffusion就是这样的模型，既然先定义了生成器再去找对应的后验很困难，不如我们先定义后验，再去适配生成器，这样就能避免优化变分后验，而是直接优化生成器，通过前向扩散为生成过程大致指定了路径，从而大大减小了生成器的搜索空间。

Score based

上一小节最后得到的逆SDE中有一个看起来很有趣的函数，这其实就是score function了:p

如果我们想要从一堆杂乱无章的噪声中通过逆向SDE得到我们目标的分布，我们需要知道score function的形式，而这也正是一个chicken and egg problem：

Why is this difficult? We don’t know p(x,t)! If we did, we could just sample from it directly instead of doing reverse diffusion.

虽然本质上我们需要的信息，但是从score function的角度出发，相比直接去学习要更加容易，因为我们并不需要约束概率分布的normalization factor。

举个栗子，对于Wiener Process，对应的score function为：

Langevin dynamics

当我们学习到了score function的参数化表示，让我们考虑如何从目标分布中采样，一个自然的想法其实是按照inverse SDE逐步得到原样本，我们需要自己来设计这个inverse SDE，这个思路留到后面的章节介绍。

这节主要介绍一种基于score function采样本身就有着一种来源于物理学背景时代悠久的方法，称之为郎之万dynamics，但值得注意的是这并不是一种特殊的inverse SDE，而只是一种score based MCMC。郎之万dynamics这个方法本身因为并没有考虑到图像生成的一些问题，是需要我们进一步优化的，而且后面我们可以利用reverse sde以及probability flow ODE来替代这种采样的过程。但作为一种初步的尝试却是十分合适的选择，也能揭露出问题的一些本质。

郎之万方程的物理背景其实就是描述受随机力影响的布朗运动系统的演变过程，有兴趣可以自己去看看，推导也是很简单，具体的形式如下图所示，表示potential energy：

根据Fokker-Planck equation，可以写出对应的概率分布sde：

如果想要我们感兴趣的分布最后收敛，应该满足：

也就是：

得到：

也就是说如果我们想要把最后的平稳分布当成目标分布采样，就要把势能函数设置为：

这样也就得到了Langevin dynamics：

利用Euler-Maruyama method离散化，可以得到：

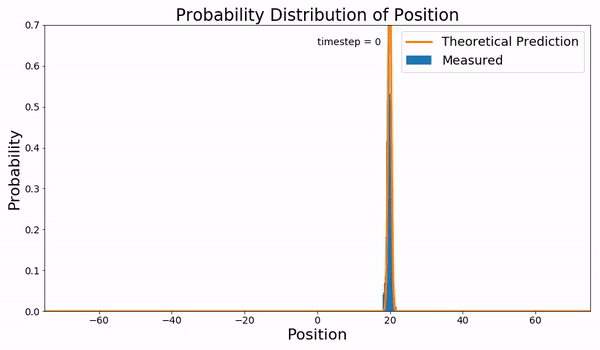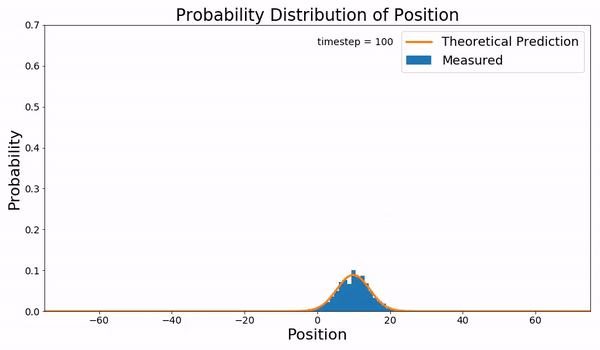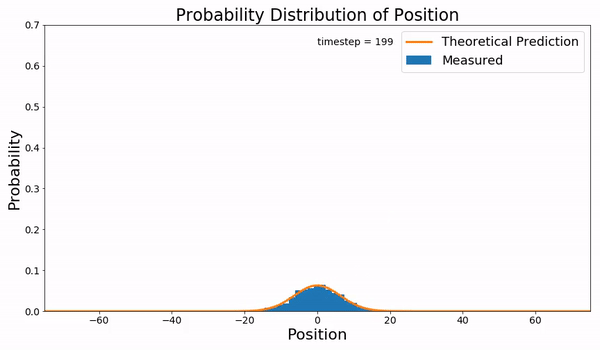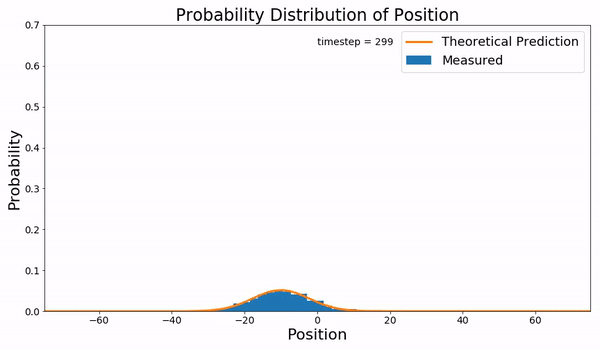
下面是对于使用 Euler-Maruyama 方法近似的具有零均值和单位方差的高斯分布随时间演变的示例：

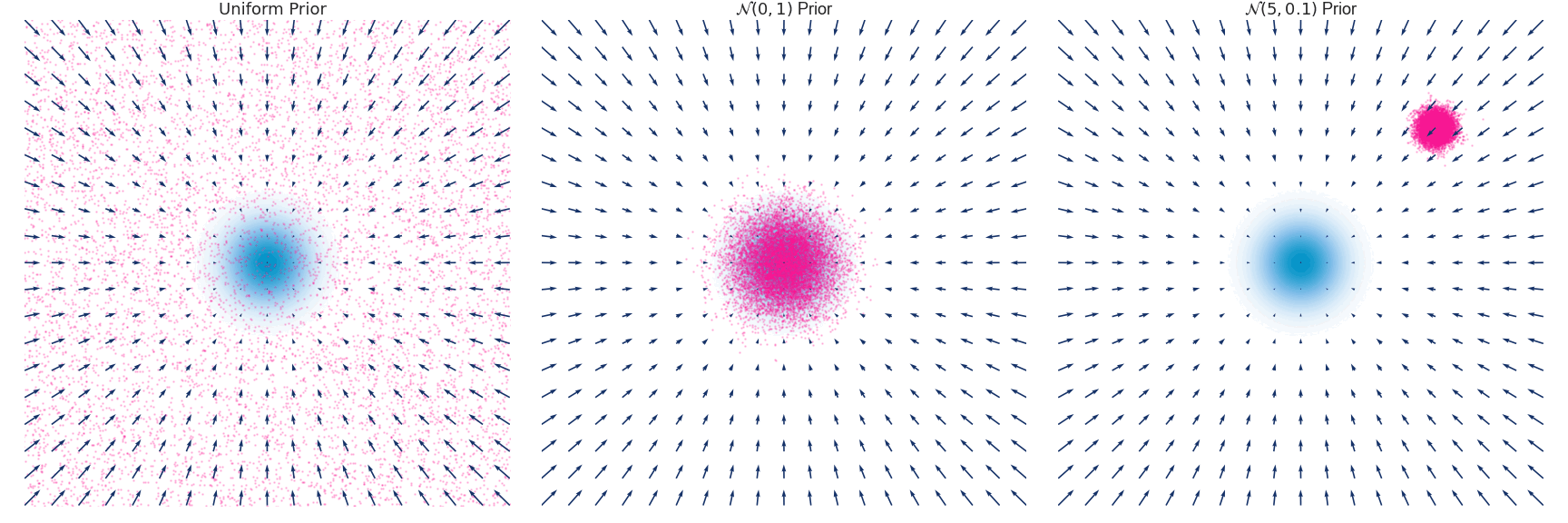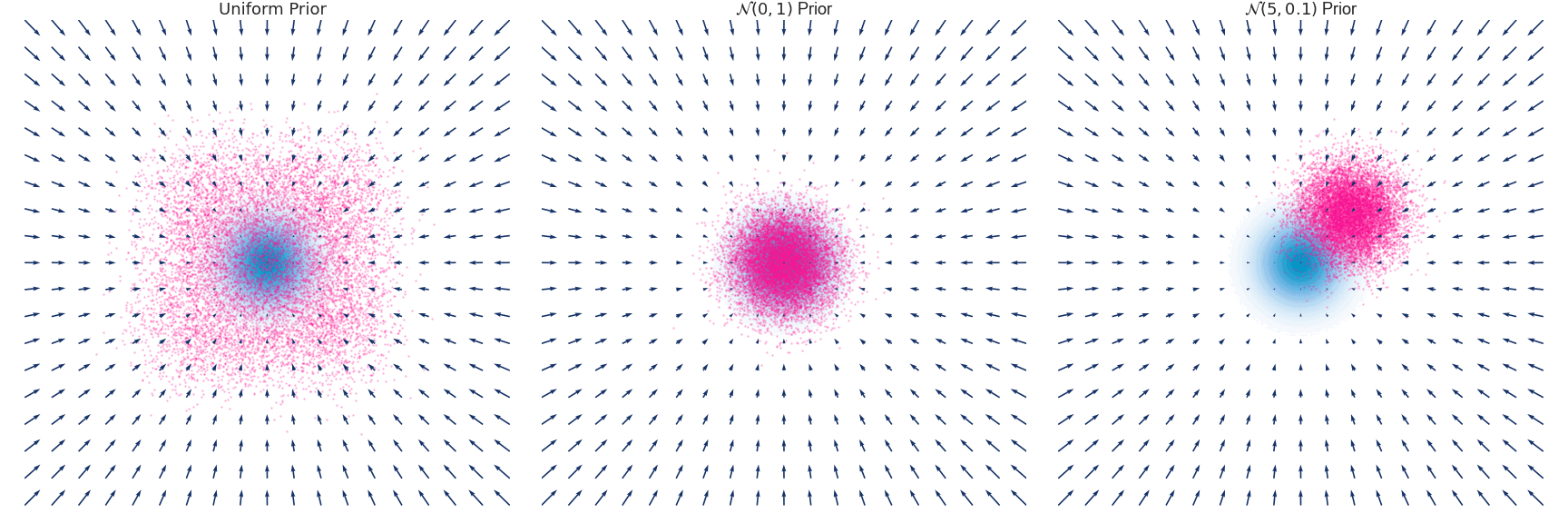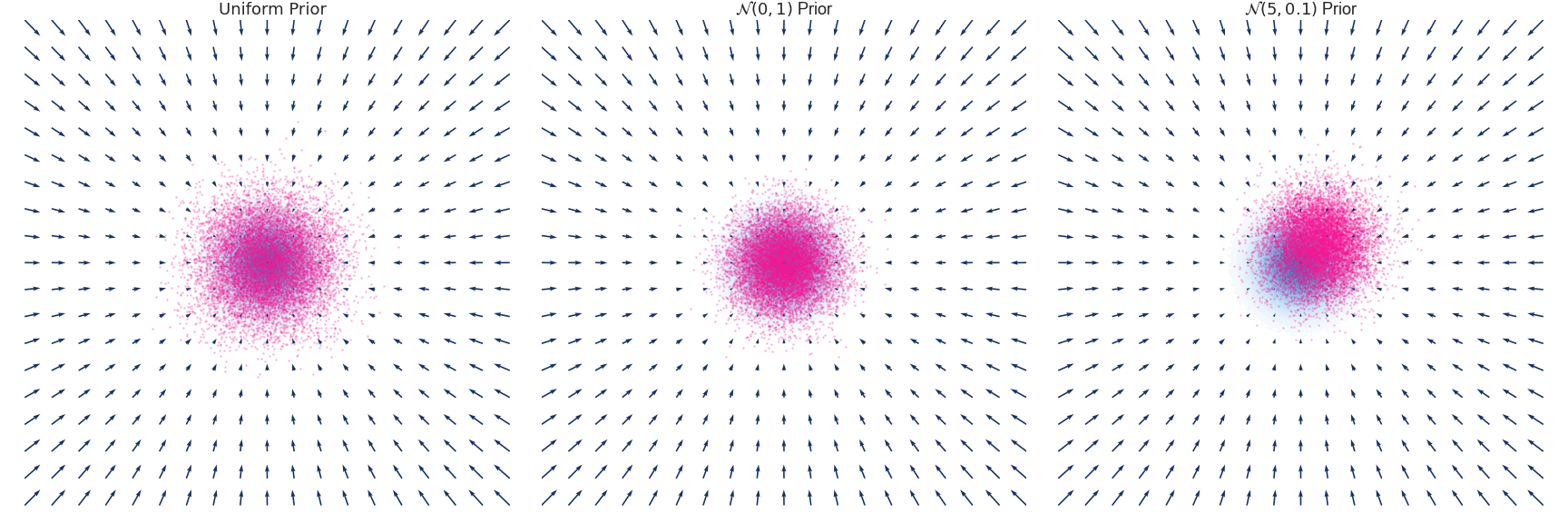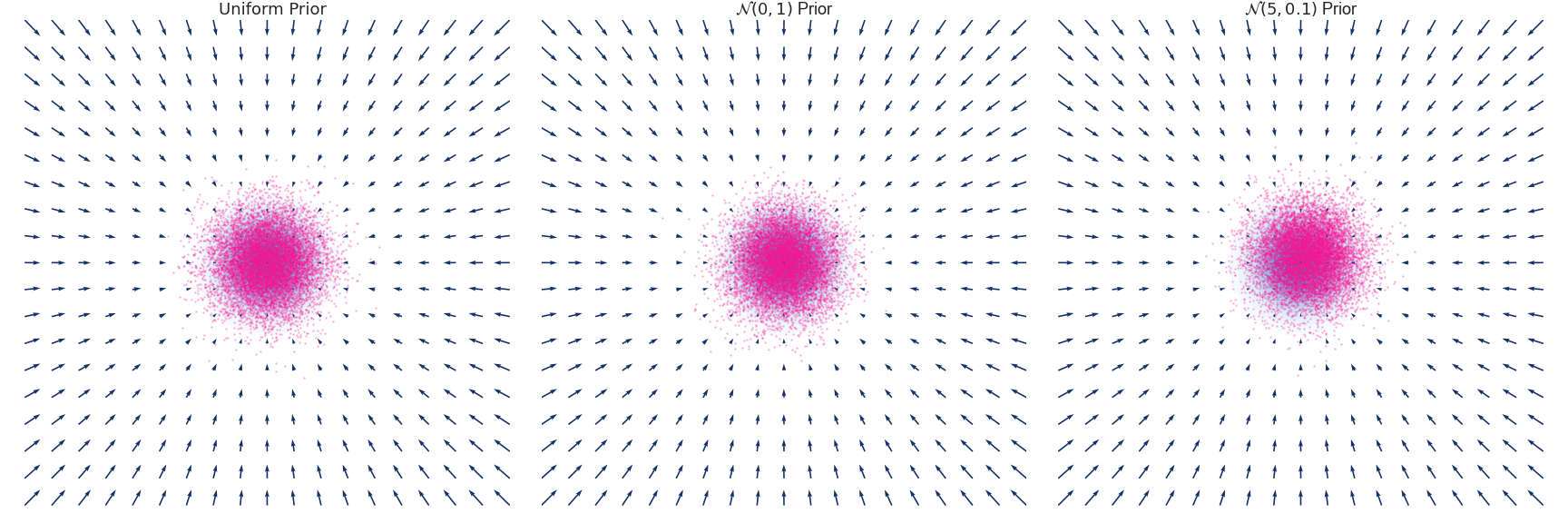
Naive Objective function

假设我们已经有了score function的参数化表示，我们想要在，上这个值域上近似目标score function，所以很容易写出一个简单的形式：

因为最终是靠sample的样本计算损失，所以不能view all sample as the same，我们需要根据的分布来计算损失，也就是求期望：

对于，我们通过分布采样的思想确定了哪些value是更容易出现的，因此对于loss的contribute要更大，对于，我们也需要考虑加上一个weighting factor指出哪些时刻是有些不同的，作用就是引入先验知识，更方便训练，最终我们得到了一个初步完善的objective function：

然而分布还是依赖于初始时刻的目标分布的，也就是，这也让求解变得棘手了起来，其他学者早已研究出如何在不知道真值的情况进行优化，这类方法统称为“score matching”，通过分布积分可以化简得到：

但是由于Jacobian通常会很大，计算代价过高，解决的方法是可以采用sliced score matching这个策略，通过random projection 得到random one-dimensional scalar fieilds来近似，简化计算量也同时保证了良好的统计性质。

Improve Langevin Dynamics

解决了训练问题，就可以用之前介绍的郎之万采样得到新的样本了：

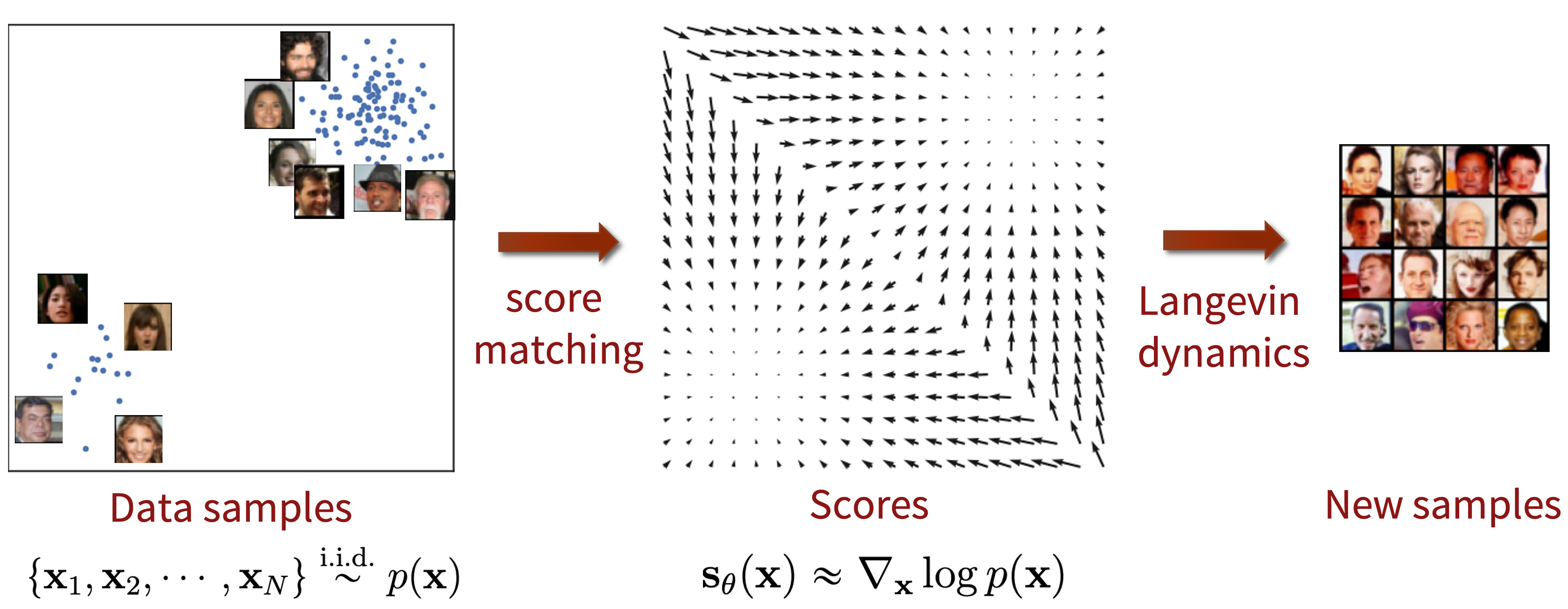
但是这也做实际的效果很差，loss 不断震荡，原因是：

低密度区域的样本太少，估计就会不准确，甚至某些采样点的概率可能为0，那么取对数就没有意义。
生活中的真实数据大部分都倾向于分布在低维空间中，这也是大名鼎鼎的 “流形学习”(mainfold learning) 的大前提。也就是说，我们的编码空间(通过神经网络等一系列方法)的维度可能很广泛，但是数据经过编码后在许多维度上都存在冗余，实际上用一部分维度就足以表示它，说明实质上它仅分布在整个编码空间中的一部分(低维流形)，并没有“占满”整个编码空间。分数这个东西： ，是针对整个编码空间定义的，然而当我们的数据仅分布在编码空间的低维流形时，分数就会出现“没有定义” (undefined) 的情况。score matching 的训练目标是基于数据“占满”了整个编码空间这个前提下而推出来的。当数据仅分布在低维流形中时，score matching 的方法就不适用了，因为undefined区域的score不能提供任何有用的信息。
朗之万动力学无法正确衡量不同mode的权重

所以一个自然的想法就是对原数据分布进行扰动，加入高斯噪声，就减少了零概率的出现，使得低密度区域也有了更多的样本。高斯噪声是分布在整个编码空间的，因此，扰动后的数据就不会仅“驻扎”在低维流形，而是能够有机会出现在整个编码空间的任意部分，从而避免了分数(score)没有定义(undefined)的情况，同时使得 score matching适用，这就破解了“loss 不收敛”的困局。这里还有一点mode-seeking转成mode-covering的味道。

而这里如何确定噪声的大小就成了问题的关键，目前提出的是加一系列不同尺度的噪声，然后分步训练每一尺度的score matching网络，具体过程是先引入一系列噪声，，这里选取noise的原则是：

Maximum noise scale: 应该取为数据点间的最大距离
Minimum noise scale: 应足够小以控制最终样品中的噪声
相邻噪声尺度应有足够的重叠，以促进退火朗之万dynamic中噪声尺度的过渡。

一种尝试就是让之间满足几何级数的关系，然后就可以得到对应的噪声扰动后的分布：

如果随机变量满足，那么，这也很好理解，条件概率相当于fix了，然后对应只有高斯的变化

这里用一个原图来帮助理解，我们要训练的是图中的箭头 (大小和方向)，随着增大，学到的箭头越来越细腻，对应的郎之万采样称为Annealed Langevin Dynamics。

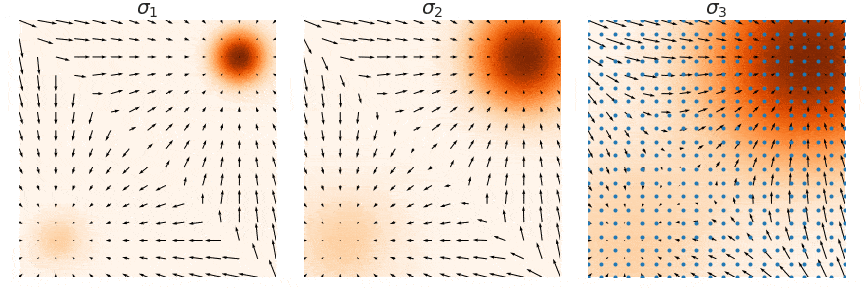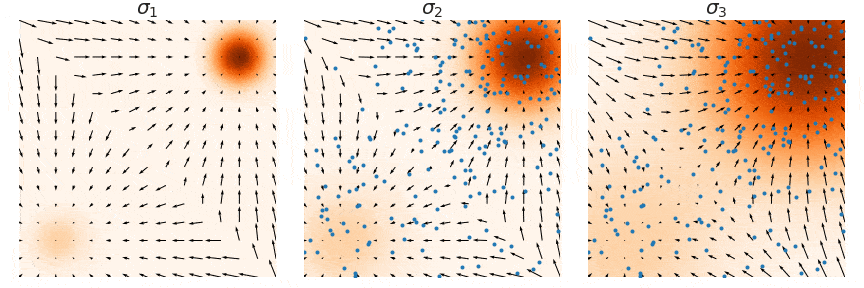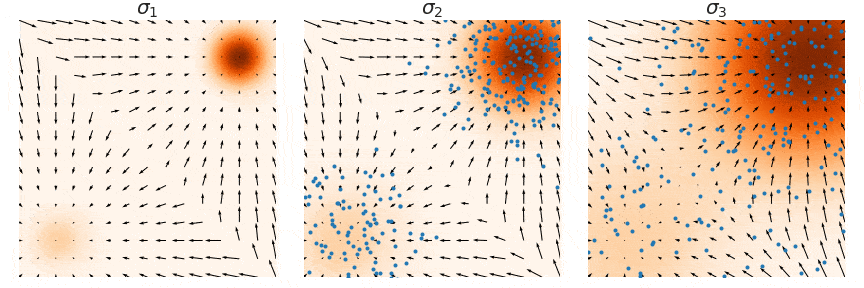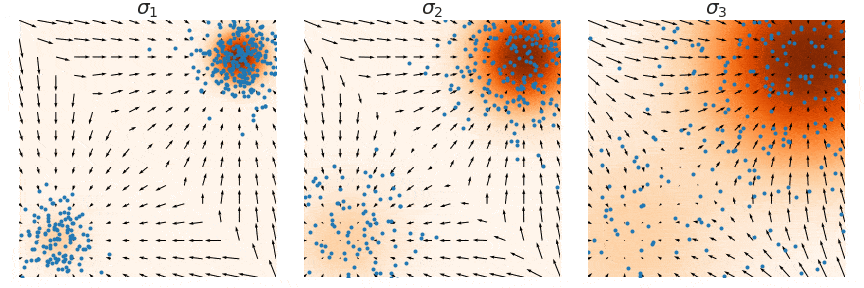
注意这里是noise sequence其实是反过来的

退火郎之万方程的motivation其实就是就是固定 “信噪比”(signal-to-noise) 的量级：

就是式子中的：

作者凭他的经验性结果告诉过我们一个结论：，于是这里就有。结合式，我们得到。这就说明，在的设置下，信噪比会固定在常量级，与噪声级别无关。

现在来看之前我们推的目标函数：

其中是一个关于的权重向量，可以引入inductive bias，也就是实现了前面说的分不同噪声尺度训练。在这种设定下，朗之万动力学采样也是分尺度来做，只不过是逆着来，从到，最后到。直觉上高噪声提供了低密度区域较好的引导，低噪声提供了高密度区域较好的引导，这样使得整个采样过程更加稳定。这个过程就称之为denoising score matching 。

Final Objective function

虽然不能直接得到目标分布的信息，但是我们可以通过条件概率引入噪声间接获取关于目标函数分布的关系，最终达到相同的gloable minim，让我们推出最终的Denoising score matching Loss Function：

需要特别说明的是，随时间的期望是根据 [0,T] 上的均匀分布得出的。

此外，还有和KL div的联系，表示逆向初始采样的分布：

下面我会介绍利用采样的样本计算目标函数值的流程，给定一个来自目标分布的样本:

从均匀分布采样
利用我们已有的转移概率信息去采样
利用已有的转移概率信息去计算

这样我们就得到了近似：

因为通常我们把转移概率定义为和指数相关的简单分布，所以实际上score function value还是很容易计算的，对于之前的Wiener Process来说，我们有:

Combine SDE with Score

到目前为止其实主要介绍了score based的一些method，但是这些方法并没有和SDE建立本质的联系，也就是并没有强调对于前向和逆向SDE建模，只是用了MCMC采样这样的策略，接下来我会介绍如何从SDE的视角结合score进行建模。

对于SDE的设计，通常都是hand designed，songyang给出了几种常用的SDE：the Variance Exploding SDE (VE SDE), the Variance Preserving SDE (VP SDE), and the sub-VP SDE，对于解reverse SDE，最简单的想法就是利用Euler-Maruyama method，也就是离散的SDE去迭代，虽然郎之万不满足reverse SDE的形式，但是它和Euler-Maruyama reverse SDE都是利用score function去迭代，这是它们的相似之处，除了Euler-Maruyama method，解reverse SDE数值方法还有Milstein method, and stochastic Runge-Kutta methods。

考虑到我们只关心的是，在不同时间步长获得的样本可以具有任意相关性，并且不必形成从反向 SDE 采样的特定轨迹。我们可以应用 MCMC 方法来微调从数值 SDE 求解器获得的轨迹。具体来说，songyang提出预测-校正采样器。预测器可以是任何能够从现有样本预测的SDE 求解器，校正器可以是任何仅依赖于得分函数的 MCMC procedure ，例如 Langevin dynamics。

Probability flow ODE

ODE其实就是把SDE中的stochastic diffusion项去除，只留drift coefficient项：

songyang在paper附录D中给出了每个扩散过程都有对应的确定性ODE的形式使得其边缘分布与SDE一致的证明，以下是其一般形式（注意其和SDE形式的高度相似，如score function的系数不同，删去了噪音项）

这是因为概率流 ODE 提供了从噪声分布到数据分布的确定性映射，反之亦然。这样做，我们基本上可以摆脱朗之万动力学采样，并用概率流 ODE 完全取代它，不难看出，我们可以把概率流 ODE视为一类continuous normalizing flow。

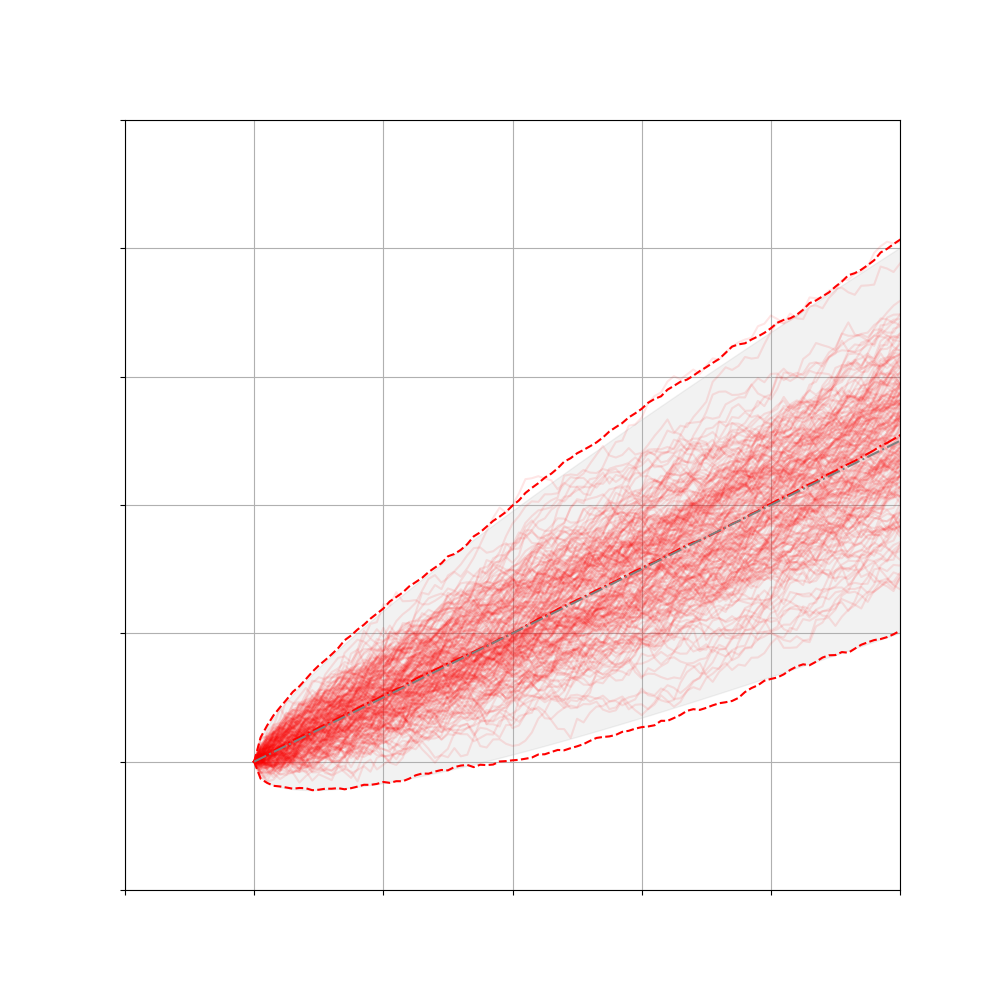
下图描述了 SDE 和概率流 ODE 的轨迹。尽管 ODE 轨迹明显比 SDE 轨迹更平滑，但它们将相同的数据分布转换为相同的先验分布，反之亦然，通过求解概率流 ODE 获得的轨迹与 SDE 轨迹具有相同的边际分布。

尽管能够生成高质量样本，但基于 Langevin MCMC 和 SDE 求解器的采样器无法提供计算基于分数的生成模型的精确对数似然的方法，而只能计算ELBO。而基于ODE的采样器却可以进行精确的似然计算，也就是说diffusion model同时可以定义一个概率流 ODE，它可以被用来做密度估计和似然计算（原因可以去看大名鼎鼎的Neural ODE，这个是关于深度学习本质的理论，这里就不多介绍）。

Special Case GMM

接下来我会以GMM举例，介绍如何利用DSM(Denoising score matching)，来做到拟合分布，这兼顾了Simplicity和Expressivity两方面特性：

Simplicity

概率密度和score function方便计算
在Diffusion过程中，GMM还是维持GMM形式的概率分布

Expressivity

GMM是可以拟合一切分布的 this post

GMM的一般形式为：

Score Function的形式可以直接写出来的（但是对于图像生成问题，不知道目标分布形式，就没法得到这步，这里为了演示目的，故意选择GMM的），我会选择用一个简单的神经网络来预测这个score function：

这个例子是我们先设计一个forward的diffusion过程，不断加noise，然后用已有的数据训练预测score function，根据reverse sde去得到denoise的目标分布。下面随机生成了一个GMM，并对于数据进行了可视化，并作为后续例子的目标分布：

mu1 = np.array([0,1.0])
Cov1 = np.array([[1.0,0.0],
          [0.0,1.0]])
mu2 = np.array([2.0,-1.0])
Cov2 = np.array([[2.0,0.5],
          [0.5,1.0]])

前向过程，我们设计如下的diffusion sde，其实增加noise perturbation的方法有很多种，这里选取的是类似于之前perturbing data with：

对应的离散形式就是Markov process：

最终的分布会趋近于：

x0, _, _ = gmm.sample(1000)

sigma = 5
nsteps = 200

x_traj = np.zeros((*x0.shape, nsteps, ))
x_traj[:,:,0] = x0
dt = 1 / nsteps
for i in range(1, nsteps):
  t = i * dt
  eps_z = np.random.randn(*x0.shape)
  x_traj[:,:,i] = x_traj[:,:,i-1] + eps_z * (sigma ** t) * np.sqrt(dt)

对应的逆向sde是：

离散的马尔科夫链版本是：

sampN = 1000
sigma = 5
nsteps = 400

lambdaT = (sigma**2 - 1) / (2 * np.log(sigma)) # marginal_prob_std_np(1.0, sigma)
xT = np.sqrt(lambdaT) * np.random.randn(sampN, 2)
x_traj_rev = np.zeros((*x0.shape, nsteps, ))
x_traj_rev[:,:,0] = xT
dt = 1 / nsteps
for i in range(1, nsteps):
  t = (nsteps - i) * dt # note the time fly back
  # transport the gmm to that at time $t$ and compute score at that time $\nabla \log p_t(x)$ 
  gmm_t = diffuse_gmm(gmm, t, sigma) # note the time fly back! start from the largest noise scale
  score_xt = gmm_t.score(x_traj_rev[:,:,i-1])
  eps_z = np.random.randn(*x0.shape)
  x_traj_rev[:,:,i] = x_traj_rev[:,:,i-1] + eps_z * (sigma ** t) * np.sqrt(dt) + score_xt * dt * sigma**(2*t)

依赖时间的score function定义为，我们可以用一个简单的神经网络来训练，对于时间我们需要进行特殊的编码，这里方法有很多，比如GaussianFourierProjection，然后把编码后的特征送到MLP里面就行了。

现在来看目标函数：

带入, then ：

最终有：

DDPM

DDPM As Discretization of Variance Preserving (VP) SDE

the Markov chain of the perturbation kernel of DDPM is given by

where are the noise scales, and if we take with scaled noise scales , we get

Now taking limits with , we get

where the approximation comes from the second degree Taylor expansion of . Then taking the limit of , we obtain the VP SDE

This process thus has bounded variance since is bounded.

Unified view of Diffusion Model

这部分还没写完，有空就写写 -.-

Variational Based的diffusion推导：https://arxiv.org/pdf/2208.11970.pdf

from songyang

By generalizing the number of noise scales to infinity, we further proved that score-based generative models and diffusion probabilistic models can both be viewed as discretizations to stochastic differential equations determined by score functions. This work bridges both score-based generative modeling and diffusion probabilistic modeling into a unified framework.

from thu大佬

可以证明，所谓的“去噪模型”与score function其实是等价的loss，这其实只需要用denoising score matching的一个性质就可以证明。有些文章里会出现“去噪”，而有些文章又会出现“估计噪声”，有些文章又会出现“score function”，但其实它们都是等价的参数化。这一点在Kingma发表在Neurips 2021的variational diffusion models中也有提到。