你真的理解PCA么
你好,这是一份关于PCA的介绍指南,希望看完全文后你能对PCA和他的小伙伴们有个全新的认识😃
2023/5/13: 后面关于PPCA和VAE的部分是放到了生成模型那里讲,具体没写博客,而是做了个ppt,所以这篇博客也算是完整了。
前言
说起来写这篇文章原因,一方面是自己留个复习的记录,对PCA做个了结😋,之前总是处于复习完又忘掉,不是很有自己的体系,这次要建立一个全面而清晰的总结。另一方面是我自己本身就对PCA相关的理论有过思考和尝试,算是接触比较多。
事实上,对于某个专题写文章不是特别的容易,如何保证介绍的精准全面,又不被参考的资料影响,兼容自己的见解与特色,我想这是决定最后文章质量的关键要素吧 :)
zxr和PCA的渊源是在高中的时候,当时学完最小二乘以后我就在思考一个问题,如果把误差定义为点到直线a的距离,这样的话怎么求解?当时我自己确实也是试了,奈何数学功底太差,最后也就不了了之,但是这个问题确实是被我带到了大学,在MIT 18.06线代的课程中,我第一次知道了答案,也是这个时候,我接触到了PCA。
其实是问过hjb的,他说求导就可以,但也没写给我看,懂不懂FDUer口算的含金量👍

在后续的ML学习中,我发现PCA这个方法在不同的板块都会有对应的新形式,甚至对于PCA及其变体的学习,就反映了机器学习的一般框架模式,颇有一种“见一叶而知深秋,窥一斑而见全豹”的感觉。
Intuition
对于现实中记录的数据,当我们想要从中发现新规律或者想要挖掘信息的时候,往往需要考虑数据的分布情况,因为实际上记录的维度可能存在冗余,事实上,很多情况下,数据都是分布在远小于原空间维度的流形上。举个栗子,观察下面的几张手写数字,不难看出对于这种图像的数据集,只有三个变化的自由度(degrees of freedom),对应于垂直平移、水平平移和旋转。于是,数据点会位于数据空间的⼀个⼦空间中,它的本质维度(intrinsic dimensionality)等于3。

另⼀个例子来源于石油流数据集,其中只有两个自由度,对应于管道中石油的比例和水的比例(之后就可以确定天然气的比例)。虽然数据空间由12个度量组成,但是⼀组数据点会近似位于这个空间内的⼀个⼆维流形当中。在这种情况下,流形由几个不同的片段组成,对应于不同的流的形式,每⼀个片段都是⼀个(带有噪声的)连续⼆维流形。如果我们的目标是数据压缩,或者对概率密度建模,那么利用这个流形结构是很有用的。
在实际应用中,数据点不会被精确限制在⼀个光滑的低维流形中,我们可以将数据点关于流形的偏移看做噪声。我们的目标就是去寻找这样的一种数据”最佳“呈现方式,而这存在至少两个视角去分析:第一种是用原数据进行变换,得到对应假设下的最优表示,去除冗余和噪声。第二种则是从生成的角度,其中我们首先根据某种隐变量的概率分布在流形中选择⼀个点,然后通过添加噪声的方式生成观测数据点。噪声服从给定隐变量下的数据变量的某个条件概率分布。
但无论是基于哪种视角提出的方法,都是遵循一定假设,符合某种物理实际情况的,PCA也不例外。现在就让我们跳出Big Picture的感知,从现实遇到的一些特定问题来引出PCA的故事 :)
Introduction
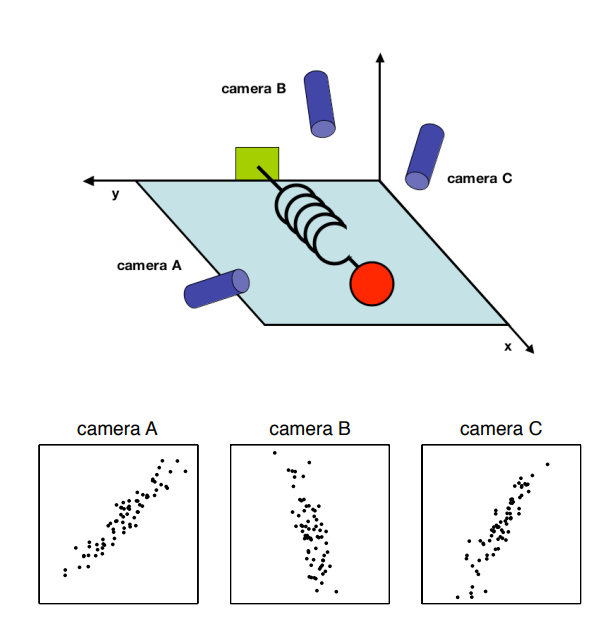
想象一下你回到了高中时代,这节物理实验课的主题是弹簧,你用了3台摄像机记录了弹簧伸缩的过程,所以你现在得到了3组数据,每组都记录了2维的坐标,所以整体上你拥有了维度是6的若干个采样点。
现在你的老板要求你挖掘弹簧伸缩遵循的背后规律,how do you get from this data set to a simple equation of x?
显然如果直接利用这个6维的数据来说明一个维度的变化规律,相对会很繁琐,所以是要对原数据去进行一些预处理的,我们需要考虑的因素有:数据的噪音和数据的冗余性。
因为理论上上弹簧的运动轨迹肯定是条直线,所以要对实际数据去噪,这个思路就是寻找方差最大的轴,方差最大对应的信息保留通常也是最大的。
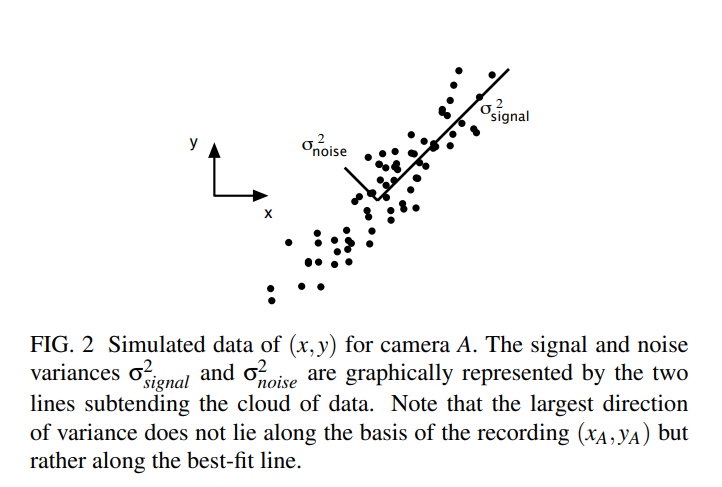
其次是数据记录的冗余性,记录的3组数据实际上是强相关的,而且对于每组数据里面的坐标变量,也会存在一定的相关性,我们的目标就是去发现并消除这种冗余性,这里我们只去消除correlation(如果是independence的话就是ICA的思想了)。

我们考虑的情况框定在线性假设下,这使得我们的目标变为:
Is there another basis, which is a linear combination of the original basis, that best re-expresses our data set?
更好的数据表示应该是在原数据空间中选择一组更好的基,使得数据在这组基的表示下相关性最小,并且我们可以按照方差的大小来对基进行筛选,达到降噪的效果,得到更好的数据表示。
Linear Algebra
博主贴心地准备好了数学扶贫资料,这里是PCA所涉及到的线性代数内容,如果你已经了解,那就可以直接看下一章节~
向量
默认都是column vector,数据矩阵的维度是
的,也记作
。
协方差矩阵
数据矩阵表示如下:
和
是两个随机变量(suppose iid),则它们的协方差定义为:
这个定义和方差很像,只不过是描述的是变量之间的关系,而不是变量本身分布。
和
的相关系数定义如下:
协方差矩阵是针对维度间的,而不是样本间的,所以最后求出来的协方差矩阵维度是的。
上面用
的原因是无偏估计,有兴趣可以自己找些资料看,这里推荐mit 6.041概率论。
接下来介绍协方差矩阵和相关系数矩阵的关系:
correlation matrix,
covariance matrix,
diagonal variance matrix
上式中的矩阵 是包含了每一个attribute的方差的对角矩阵。
那么,相关矩阵 和协方差矩阵
的关系如下:
可以发现,消除变量间相关性其实也是等价于变量间协方差的值为0,所以这也是为什么后面我们就用协方差去分析。
SVD分解
参考18.06的引入,对于一般的矩阵,如果
有
个线性无关的特征向量,那么可以得到特征值分解
,而对于实对称矩阵,可以分解为正交矩阵和对角矩阵乘积的形式
,那么会不会存在一种对角正交的分解,对于一般的矩阵也是适用的呢?其实SVD就是反映了这样性质,下面我会逐步引入介绍 :)。
首先介绍一下比较一般的特征值分解:
给定矩阵 的
个线性无关的特征向量,按列组成方阵,即:
那么有
其中 为特征值组成的对角矩阵,因为假设组成特征向量矩阵
的
个特征向量线性无关,所 以
可逆,从上式中就可以推导出对角化以及特征值分解的公式:
接下来介绍一下对阵矩阵的特征值分解:
对于实对称矩阵 ,存在实数
和向量
使得
是
的一个特征值,
是对应的特征向量。如果
有两个不同的特征值
和
, 对应的特征向量分别是
和
,
由于, 我们可以得到
, i.e.,
和
是正交的。
对于, 我们可以找到
个特征值以及
个特征向量,所以,
可以被分解为
是个正交矩阵 (i.e.,
) ,
. 我们可以将
表示成列向量形式:
那么:
这里 是
的一组正交基。
那么SVD其实就是这样的一种矩阵分解技术,对于任意的矩阵都可以找到对应的正交对角分解,具体的推导由来可以看:link,由和
的特征值和特征向量引出的构造性证明。
根据矩阵乘法的几何意义,每个线性变换都可以分解为如下的旋转拉伸旋转操作,实际上可以变换到高维空间(和
的维度可以是不同的,因此最后
的变换是可以到高维的subspace),这里只展示二维的过程。

可以将矩阵 视为一种线性变换操作,将其行空间中的一个向量
,变为其列空间中的向量
。奇异值分解就是要在行空间中寻找一组正交基,将其通过矩阵
线性变换生成列空间 中的一组正交基
。
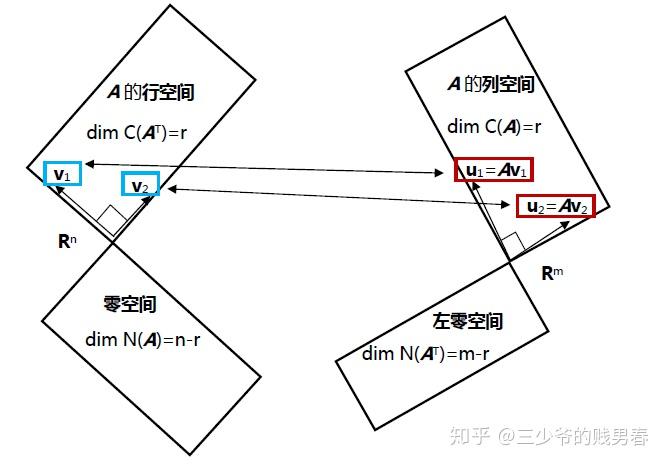
对于SVD中的那三个矩阵的求解,可以采用如下的方法:
其实就是求这俩对阵矩阵的特征向量和特征值就行了。
PCA和SVD都能用于求解Col X的basis,而且它们求解出来的basis可以‘认为’是同一个。两种方法的理论出发点不一样,PCA是从出发,考虑的是change of variable,目的是使的替换之后的variable是uncorrelated,即新的covariance matrix是对角阵。SVD是从
出发,矩阵分解时得到Col X的一个basis,而该basis也可以验证得到是
的eigenvectors set。两者都是建立在symmetric matrix对角化分解理论的基础上。SVD计算得到的basis更多是算一种副产品,主要目的是matrix decomposition,PCA的目的就是找basis。在计算时,PCA一般也是用SVD来计算。
基变换
我推荐看3b1b的:link
PCA
Intuition
假设数据已经中心化
假设就是线性,具体来说就是我们想要找的基是由原基向量线性组合得到的,让我来复述一下我们的目标:
- 最小化冗余,这里的冗余我们认为是变量间的协方差
- 最大化信息,这里的信息我们认为是变量的方差
也就是说,对于在新基下的数据表示,我们希望协方差矩阵是对角化的,off-diagnoal的元素都是0,达到去相关(decorrelated)。实际上有很多方法(变换)可以使得变换后的数据去相关,而PCA选取新的基向量都是orthonormal的,这个原因其实是根据数学证明来的(后面会提到),暂且我们可以先认为是为了简单和方便起见,因为orthonormal matrix可以认为是旋转让新的坐标轴和最大方差的方向对齐,就像在Introduction章节里的那张图一样。
这里说的最大方差是在当前假设下,投影得到的最大方差,没有任何假设下的最大方差的轴向可能不是正交基向量的方向,这个后面会说,也就是ICA。
假设我们进行变换后得到的数据向量表示是,设我们的基向量组成的
orthonormal matrix为,那么就有
,此时得到的
的协方差矩阵为:
而我们知道每个对称矩阵都有对应的正交对角分解,如果我们就取 分解得到的正交矩阵为
,那么则有:
嘿!这不就是我们想要的结果么,变换后的协方差矩阵已经变成了对角化😀,我们的目标达成了,这样的就是我们要找的新的基向量矩阵,而具体对于
的计算可以通过协方差矩阵的SVD得到 :)
不妨让我们再挖掘更深一些,这样得到的数据表示能不能为我们提供一些分析处理数据的insight,比如dimensional reduction,以及对于选取的主成分(基向量)的解释,是否确实是满足了投影方差最大化,保留了最多的信息。
这就需要我们去明确定义一些优化问题,以降维为例,我们需要定义什么是一个好的结果:
we must define what we consider optimal results. In the context of dimensional reduction, one measure of success is the degree to which a reduced representation can predict the original data. In statistical terms, we must define an error function (or loss function). It can be proved that under a common loss function, mean squared error (i.e. L2 norm), PCA provides the optimal reduced representation of the data. This means that selecting orthogonal directions for principal components is the best solution to predicting the original data.
最大方差
考虑观测到的数据集,每条数据都是长度为
的向量,我们的目标是把数据投影到一个维度为
的子空间,使得投影后的数据方差最大,假设
是已知的(后面会介绍可以自动确定
的方法,但是普通的PCA是需要提前确定,毕竟没有关于这方面的假设)。
首先让我们考虑投影到一维的子空间,也就是,用长度为
的单位向量
表示这个空间的方向,
,因为我们只关心方向,而不在意
的大小,这样的话每个数据
就可以投影到这个子空间内,得到一个标量
,原数据的均值投影后可以得到
。
是样本的均值:
投影后得到的方差可以定义为:
是原数据的协方差矩阵:
我们现在想要改变,得到最大化投影方差
。显然这需要是一个约束优化问题,为了防止
。而一个合适的约束条件,正是我们上面所定义的
。为了强制这个约束条件生效,我们引入拉格朗日乘子
,讲约束优化问题转为非约束最大化的形式:
取关于 的梯度为0,我们可以得到一个驻点满足:
这说明 必须是
的特征向量,如果我们在左侧乘上
,利用
,可以看出方差可以表示为
。
所以为了让方差取到最大,我们可以设置为
最大特征值对应的特征向量,这样就得到了我们想要的投影方向,也称为是主成分。
类似的,我们逐步得到个主成分,这样就构建起了我们想要的子空间,以及数据的表示。
最小重构误差
现在我们来从最小投影误差的角度讨论,首先引入一个维的完备正交标准化基向量集
,满足
因为基是完备的,所以数据点可以表示为基向量的线性组合:
系数 对于不同的数据点是不同的。 这对应将原坐标系旋转到由
定义的新的坐标系下,原始的
个分量
被一个等价的集合取代
. 和
取内积,利用正交标准化的性质,我们得到
,不失一般性,我们写成如下形式:
我们的目标是只用限定数量 个变量的一种表示方法近似这个数据点,对应于低维度子空间的一个投影。不失一般性,
,维线性子空间可以由前
个基向量表示,,所以我们可以如下近似每个数据点
:
依赖于特定的数据点,
对于所有数据点都是一样的(子空间),对于
、
和
我们可以任意选择,从而最小化由降维导致的失真。作为失真的度量,我们使⽤原始数据点与它的近似点
之间的平方距离,在数据集上取平均。因此我们的目标是最小化
首先考虑关于 的最小化,带入
,将关于
的导数设置为0, 利用正交标准化的条件,我们可以得到:
其中 类似的,将
关于
的导数设置为0,再次利用正交标准化的条件,可以得到:
其中。如果带入
和
,利用上面
和
的展开式可以得到:
从中我们看到, 从 到
的位移向量位于与主⼦空间垂直的空间中,因为它是
的线性组 合,其中
。这与预期相符,因为投影点
⼀定位于主子空间内,但是我们可以在那个子空间内自由移动投影点,因此最小的误差由正交投影给出。
于是,我们得到了失真度量(其实也就是重构损失) 的表达式,它是⼀个只关于
的 函数,形式为:
接下来就剩下关于
的最小化了,这显然是个约束优化问题,否则就会得到
这样不合理的解,约束来自之前正交标准化的定义。
推导出正式的结果之前,让我们用一个简单的例子来获取一些直观的感受,考虑的数据空间,以及
的主成分子空间(
principal subspace,也就是由主成分向量张成的空间),我们要选择一个方向来最小化
,满足约束
,用拉格朗日乘子法就可以得到如下的表达式:
将关于 的导数设置为0,我们可以得到
,所以
是
具有特征值
的特征向量。 因此任何特征向量都是上面重构误差的一个驻点。为了找到
的最小值,我们将
回代到上面的重构误差中得到
。于是,我们通过选择
成为两个特征值中较小的对应的特征向量,得到了
的最小值。 因此,我们应该将主子空间与具有较大的特征值的特征向量对齐。这个结果与我们的直觉相符,即为了最小化平均平方投影距离,我们应该将主成分子空间选为穿过数据点的均值并且与最大方差的方向对齐。对于特征值相等的情形,任何主方向的选择都会得到同样的
值。
在一般的情况下,也就是对任意 和
,可以通过选择
为协方差矩阵的特征向量来最小化
:
其中,特征向量
和往常一样选成正交标准化的。 重构误差的值相应可以表示为:
其实也就是正交于主成分子空间的特征向量的特征值之和,因此我们可以通过选择个最小的特征值对应的特征向量来最小化
的值,因此组成主成分子空间的特征向量就是最大的
个特征值所对应的。
尽管我们考虑的是,事实上对于
也是成立的,只是没有降维,仅仅对原坐标系做了旋转,和主成分对齐。
统一的视角
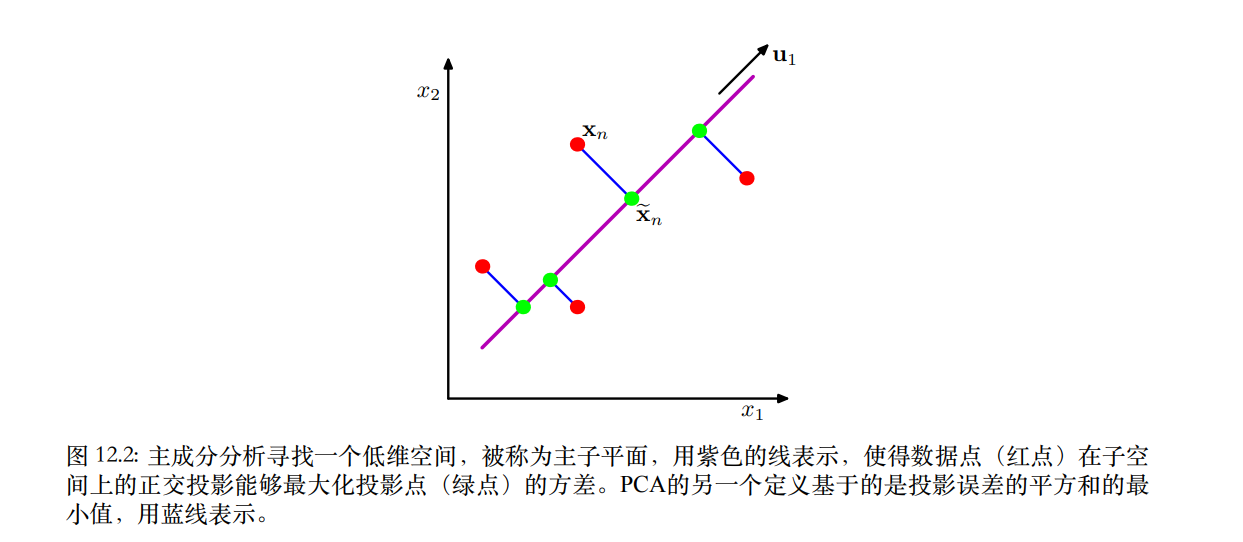
上面的两种定义和之前我们提出的Intuition的解法是一致的,这说明PCA是兼顾这三者的性质。那么不妨再深入的想一想,为什么最大方差和最小重构误差是等价的,从直观的感受和数学推导两个角度应该如何说明。
下面这张图很清晰的展示了方差和重构误差之间的联系,其实就是高维的勾股定理:
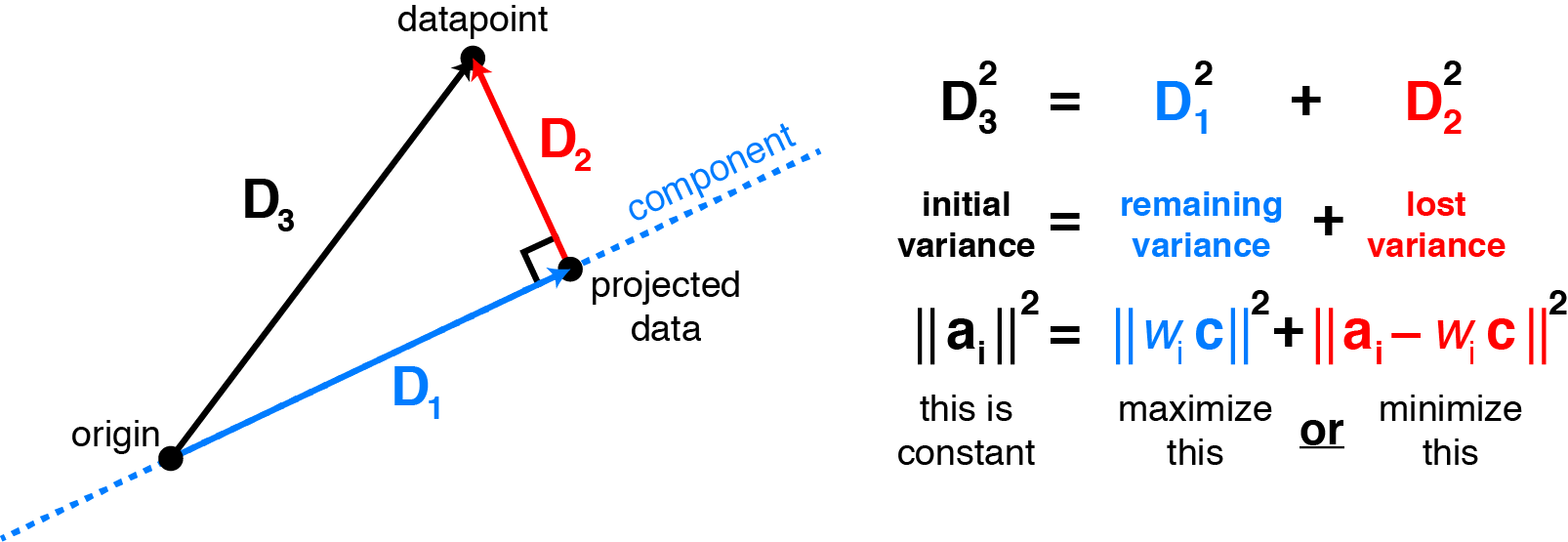
我们知道是
在
方向上的投影,因此
、
可以视为直角边和斜边,对应上面图里的
和
,而
也就是对应
了。(origin其实就是中心点)
直观上的理解就是这样,对应的数学推导也自然能写出来(这里默认已经中心化了):
参考:http://alexhwilliams.info/itsneuronalblog/2016/03/27/pca/
High Dimensional data
事实上,在许多实际应用中,我们只能获取数量有限,而维度又很高的数据,对于这种数据的分析往往是比较困难,因为很多机器学习的方法都是基于矩阵和逆运算的,而小批量高维的数据,它的一些统计量矩阵是不可逆的,此外运算的开销也和数据的维度有关,高维往往会来带不可实现的计算量。但对这种数据的分析又是极为重要的,我们就要去思考创造一些对应的策略。
不知道大家有没有过这种经历,对于的数据应用PCA,如果你想要降维到
维,
,用
sklearn的话,实际上调库返回的降维后只有维,因为在⼀个
维空间中,
个数据点(
定义的一个线性子空间,它的维度最多为
,实际上,如果我们运行PCA,我们会发现⾄少
个特征值为零,对应于沿着数据集 的方差为零的方向的特征向量。
如果将PCA应用于几百张图片的数据集,每张图片是对应的向量是几百万维,要知道通常对于寻找 矩阵的特征向量的算法是
的,实际中这显然不可接受。
针对这种情况的解决方法其实很简单,如果你有仔细了解过SVD相关的知识的话,不难想到我们的目的就是得到的特征向量,其中
是
维中心化后矩阵,而
可以看做是把行空间的基
变换到列空间的基
,但同时进行了一定的长度拉伸,这里的
对应的是
的特征向量,而
对应的是
的特征向量。也就是可以写作
,其中的
是对应的系数,根据SVD分解得到的
中的
就能确定
的值了,不难得到$c={1\over \left(N \lambda_i\right)^{1 / 2}} $,这样就把 $ O(D^3)$ 的计算转换成了 $ O(N^3) $。
为了严谨性,我还是再推一遍:
两边乘上 得到
我们定义 ,得到
这是 矩阵
的一个特征向量的方程。我们看到这个矩阵与原始的协方差矩阵具有相同的
个特征值,原始的协方差矩阵额外含有
个为0的特征值。因此我们可以在低维空间中解决特征向量计算的问题,计算代价是
而不是
。为了确定特征向量,我们将上式两侧乘以
得到:
我们可以从中看出 是
的一个特征值为
的特征向量。但是注意,这些特征向量长度不一定是1,为了确定合适的归一化,我们需要一个常数来对
重新规范,使得
, 假设
长度已经归一化,那么我们有:
总结⼀下,为了应⽤这种⽅法,我们⾸先计算 ,然后找到它的特征向量和特征值,之后利用上面的公式计算原始数据空间的特征向量。
Applications of PCA
Whitening
白化其实就是定义了一个满足如下性质的变换:
- 消除了特征之间的相关性
- 所有特征的方差都为 1
是不是感觉很熟悉,只要把PCA的步骤稍作改动就可以了,首先我们定义:
是
对角矩阵,对角元素是
,其实就是
is a
主成分正交矩阵
。 然后我们对每个数据点
定义一个变换:
很显然 的协方差矩阵是单位阵:
这样的 就是白化后的数据了。
Mahalanobis Distance
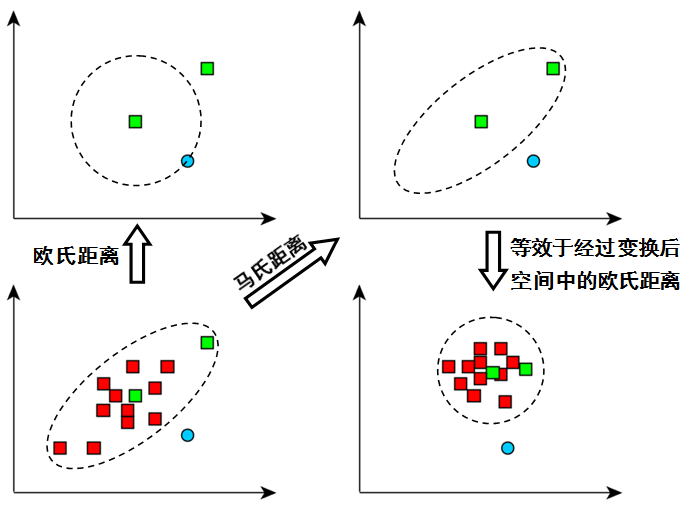
马氏距离定义为:
其实可以看作是,,和白化如出一辙:
因此马氏距离可以理解为白化后数据的欧几里得距离。
Limitations
然而当我们尝试着用PCA解决下面的两种问题时,似乎PCA看起来失效了,也就是并不符合我们想要的预期,这是由于什么原因呢?(注意B图实际上主成分方向有点问题,应该是两条数据线之间的)

因为我们之前的假设只是去相关,而变量间更高层次的依赖关系并没有完全去除,因此有时候,只是去除相关关系对于揭示数据的结构是不够的,这就启发我们去寻找解决新问题的方法。
去除更高层次依赖关系的方法有很多,如果对问题有着先验的知识,我们可以尝试kernel method,例如上图中的A,可以用极坐标表示数据。也可以直接去除变量间的dependence,这就是ICA的想法,可以用来解决上图中B的问题。
接下来就让我们介绍PCA的这种变体,也就是Kernel PCA。
Kernel Tutorial
鸽~
Kernel PCA
鸽~
PPCA
Multivariate Gaussian
2022/11/26 昨天开完组会,老师讲了一下多元高斯,有种高中去补习数学的感觉hh,然后发现这个内容本身和这篇blog很贴合啊,就放到这里总结一下了。
多元高斯分布是Probabilistic ML的一个重要基础,也和PPCA有着很强的联系,所以这个小结来介绍一下MG :)
对于一维的高斯分布,想必大家都是很熟悉了:
通过归一性可以计算出前面的系数,计算的方法是用到了二重积分,也就是 换元以后平方处理,其实就相当于引入另一个轴上的高斯分布,凑一个圆的表达式,再换极坐标系积分。
对于高维的高斯分布,形式是这样的:
显然这个分布的系数不是很容易想到,肯定是要具体积分算出来的,但是高维的积分直接处理起来会很困难,因为含有 这种matrix,之前的section有说过一种叫做白化的方法,其实也不一定非要像白化那么彻底,我们只要消除变量间的相关性,也就是把这个cov matrix变成对角阵的形式,这样计算就会大大减少了,因为不相关的话就可以一层层来积分了。
这里利用了这个性质:满足正态分布的随机变量X,Y,且其联合分布也满足正态分布,有X,Y 不相关 ⇔ X, Y 独立
所以我们考虑换元,这个形式之前的section用过很多遍了,看到这里你也应该会觉得很熟悉,几何上来说就是平移+旋转,这样处理的好处就是对于新坐标系下的数据
,其协方差矩阵是对角化的。
数据的协方差矩阵是正定的(证明link),对称性肯定是有的(实数域),就可以进行对称矩阵分解:
这里的 为什么和
中的
是一样的,我在之前的section就有说到。
因为是概率分布函数,所以换元的时候要注意再乘一个项,(intuition可以去看看mit的概率论),具体的规则如下:
其中,,
是反函数,Intuition的解释是:
两个event是相等的:
因为是算积分,所以换元的时候要注意乘上Jacobian行列式,(关于这个的intuition,我记的可汗学院的manim动画做的很不错),具体的规则如下:
综合上面的分析,在换元之后,积分内的项要多乘上两项,概率变换的 ,Jacobian matrix 其实是
,毕竟只是去rotate,最终得到的待积分式子如下:
因为这里的 是向量形式,需要进一步展开成分量
,一共
维,进而得到:
里面嵌套的 可以写做连乘的形式,由于变量间不相关(独立),因此可以单独拿出来每个做积分,也就是可以写成下面的形式:
注意到 是标准差,最后得到的结果也就是:
因此也就得到了完整的Multivariate Gaussian Distribution:
对于多元高斯分布的统计量 和
的计算,其实也是利用换坐标系的思路,具体的证明过程如下:
补充资料:https://cs229.stanford.edu/section/more_on_gaussians.pdf
写完之后才发现有教材已经给出了,XD怎么不早点给我看看 https://blog.csdn.net/luixiao1220/article/details/117321367
从最小二乘谈起
我们知道二次损失函数和高斯先验误差+MLE是等效的,具体的原因可以看:link and link、link。
但是最小二乘只是针对于scale的,而vector的情况会是怎么样的呢?不妨让我们将以上的思路进行推广,到了向量的多维空间,二次损失函数和高斯误差的联系在哪里,换句话说,PCA会不会可以从这个思路引出一个概率形式?
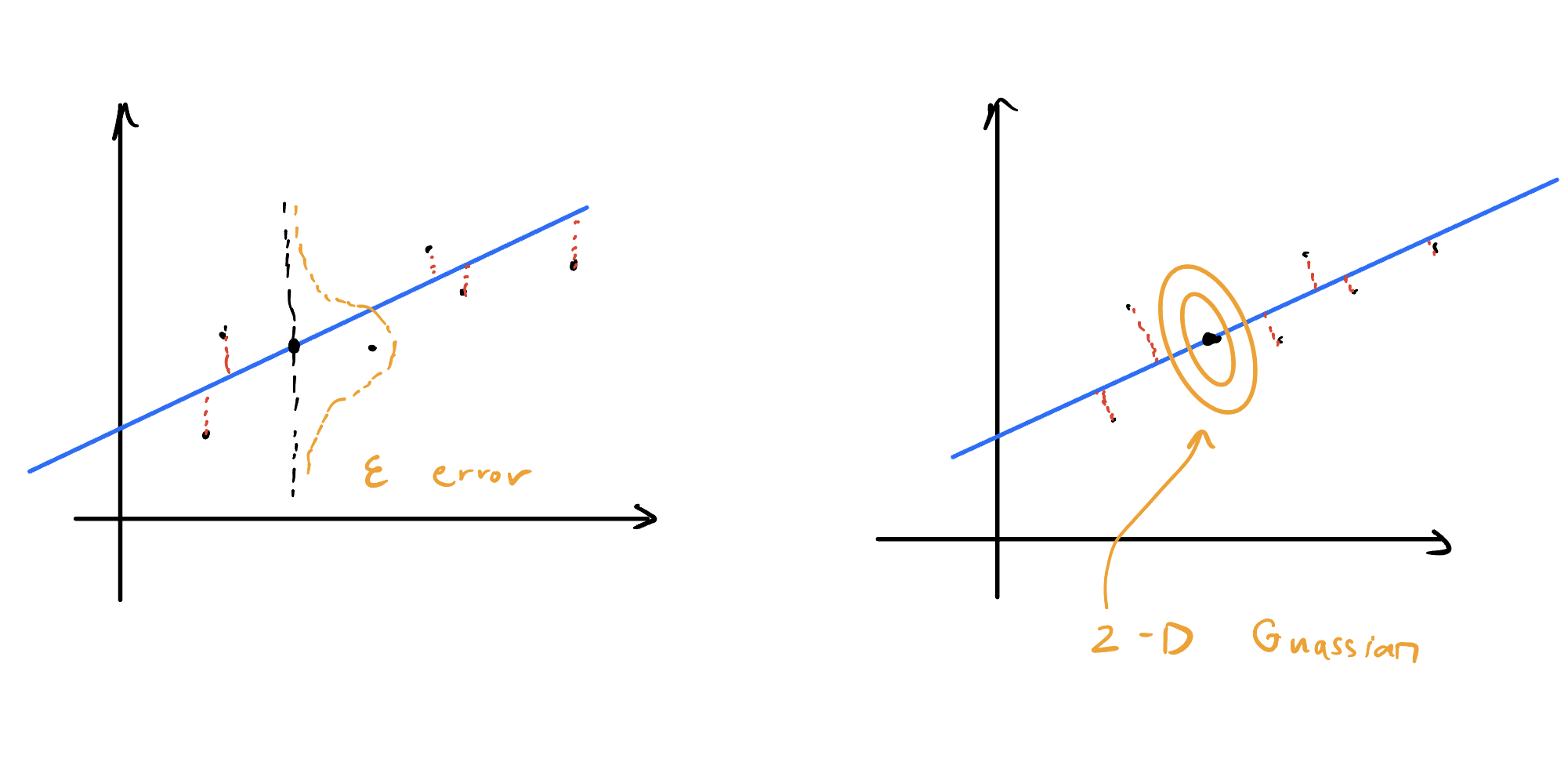
这样很自然地就从生成的角度去思考,更具体一些,也就是continuous latent variable model,隐变量的概念极大丰富了模型的可解释性和表达能力,这里默认你已经对GMM高斯混合模型有了解,你应该知道GMM是一种discrete latene variable model。所谓的continuous可以理解为隐变量是有一种连续的分布(默认你也理解了概率论的一些概念),那么有了这个idea,就让我们一步一步去尝试吧 :)
我们先引入隐变量 ,对应的应该是主成分子空间。接下来定义隐变量上的高斯先验分布
,以及观测变量
在given
下的高斯条件分布
。
的先验高斯分布定义如下:
类似的,我们定义条件分布:
的中心是
的一个线性函数,由
矩阵
和
维向量
给出。 注意,可以关于
的各个元素进⾏分解,换句话说,这是朴素贝叶斯模型的⼀个例子。
的列在数据空间中生成了线性的主成分子空间, 这个模型中的另一个参数
控制着条件概率分布的方差注意,我们可以不失⼀般性地假设潜在变量分布
服从一个零均值单位协方差的高斯分布,因为更⼀般的高斯分布会产生⼀个等价的概率模型。
我们可以从生成式的观点看待概率PCA模型,其中观测值的⼀个采样值通过下面的方式获得:首先为潜在变量选择⼀个值,然后以这个潜在变量的值为条件,对观测变量采样。具体来说, 维观测变量
由
维潜在变量
的⼀个线性变换附加⼀个高斯“噪声”定义,即
下面的图可以帮助你理解,如何把概率生成的过程,看作是一种transformation:
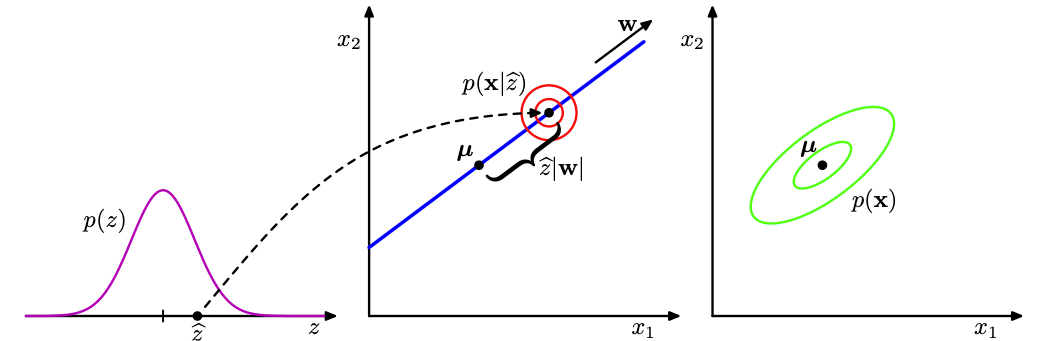
具体的数学推导我不会写了,包括PPCA的极大似然估计,EM算法等,具体可以看PRML去了解 :)
Factor Analysis
从高斯分布拟合引入问题,Andrew的那个GMM n < d的例子
GIVEN : an -by-
matrix
Assume the rows are IID samples from an unknown
.
GOAL : Estimate
Factor Analysis
Assume :
where is a length-
vector,
is a
-by-
matrix,
is length-
and
is a diagonal matrix with
along the diagonal.
If the z’s are ‘averaged out’ :
ICA
不一定有时间讲的很细了,资料在这里:
https://www.youtube.com/watch?v=ITkk6dHxh_w&list=PLXSSzzVoCfsUgrb6v5wa2ahyfu-om8B8t&index=10
[1404.2986v1] A Tutorial on Independent Component Analysis (arxiv.org)
PGM
引入PGM
Auto Encoder
AE
引入VAE,为GAN和Stable Diffusion model铺路。
后记
断断续续写了一个月还没写完的系列,别一直鸽下去勒)悲





