Dp问题汇总
DP问题汇总
总体感知
DP的学习大概分为两个大块:第一是对于原理的理解,也就是DP为啥能优化,是咋优化的,啥时候能用DP;第二就是刷题,总结掌握状态表示。
Question 1: What is DP?
DP是用来求最优化问题(optimal questions)的方法。求解最优化问题的时候,一般来说局部最优并不能达到整体最优,第一步不是很优or最优,第二步也不是,但是总体来说却可能达到最优,这也就是有些微妙的地方,这种问题基本都可以朴素的brute force,但是指数级别的代价都是ba可接受的。但是捏如果这个最优化问题具有优化子结构,那么就可以考虑DP了,通过把握优化子结构,找到状态表示,按照DP的思想,就可以得到问题的solution。
The basic idea of DP: When you are recursing on a function, it is like to get called with the same input many times. Only calculate for that input once, store it in a hash table, and then look it up whenever you need it again.
For an intuitive understanding, we can view dp as follows:

第三点的DP解释其实不是针对subprob的DAG,而是说有些DP问题的思路和shortest paths的原理很像,也就是guessing + recursion + memoization。
Question 2: Why DP can do better?
因为DP把原问题解析成了polynomial这个级别个数的子问题,所构成的DAG图,所以只要解决了每个子问题,就可以得到原问题的解,而解决每个子问题的代价*子问题数,基本也是polynomial级别的,所以DP actually does a better job.
Question 3: In which case can we use DP?
这个问题可能内容稍多,但是基本全面。
DP适用的问题是最优化问题,应用DP的前提是有optimal substructure & overlapping subproblems。
关于优化子结构,Wiki是这么说的:
In computer science, a problem is said to have optimal substructure if an optimal solution can be constructed from optimal solutions of its subproblems. This property is used to determine the usefulness of dynamic programming and greedy algorithms for a problem.
Typically, a greedy algorithm is used to solve a problem with optimal substructure if it can be proven by induction that this is optimal at each step.Otherwise, provided the problem exhibits overlapping subproblems as well, dynamic programming is used. If there are no appropriate greedy algorithms and the problem fails to exhibit overlapping subproblems, often a lengthy but straightforward search of the solution space is the best alternative.
In the application of dynamic programming to mathematical optimization, Richard Bellman’s Principle of Optimality is based on the idea that in order to solve a dynamic optimization problem from some starting period t to some ending period T, one implicitly has to solve subproblems starting from later dates s, where t<s<T. This is an example of optimal substructure. The Principle of Optimality is used to derive the Bellman equation, which shows how the value of the problem starting from t is related to the value of the problem starting from s.
然后正式的定义捏是这样的:
A slightly more formal definition of optimal substructure can be given. Let a “problem” be a collection of “alternatives”, and let each alternative have an associated cost, c(a). The task is to find a set of alternatives that minimizes c(a). Suppose that the alternatives can be partitioned into subsets, i.e. each alternative belongs to only one subset. Suppose each subset has its own cost function. The minima of each of these cost functions can be found, as can the minima of the global cost function, restricted to the same subsets. If these minima match for each subset, then it’s almost obvious that a global minimum can be picked not out of the full set of alternatives, but out of only the set that consists of the minima of the smaller, local cost functions we have defined. If minimizing the local functions is a problem of “lower order”, and (specifically) if, after a finite number of these reductions, the problem becomes trivial, then the problem has an optimal substructure.
但是实际在用的时候,不可能按照上面的理论说明来找和判断优化子结构,合理的想法是先找出一个可能是优化解结构的思路,也就是下一层问题依赖于子问题的优化解,然后再去实际地证明。
这里顺便介绍一下证明优化子结构的常用方法,也就是 “cut and paste”:
The term “cut and paste” shows up in algorithms sometimes when doing dynamic programming (and other things too, but that is where I first saw it). The idea is that in order to use dynamic programming, the problem you are trying to solve probably has some kind of underlying redundancy. You use a table or similar technique to avoid solving the same optimization problems over and over again. Of course, before you start trying to use dynamic programming, it would be nice to prove that the problem has this redundancy in it, otherwise you won’t gain anything by using a table. This is often called the “optimal subproblem” property (e.g., in CLRS).
The “cut and paste” technique is a way to prove that a problem has this property. In particular, you want to show that when you come up with an optimal solution to a problem, you have necessarily used optimal solutions to the constituent subproblems. The proof is by contradiction. Suppose you came up with an optimal solution to a problem by using suboptimal solutions to subproblems. Then, if you were to replace (“cut”) those suboptimal subproblem solutions with optimal subproblem solutions (by “pasting” them in), you would improve your optimal solution. But, since your solution was optimal by assumption, you have a contradiction. There are some other steps involved in such a proof, but that is the “cut and paste” part.
( •̀ ω •́ )✧总结起来也就是说,先找到子问题的形式(可以尝试不断扩大问题规模去找),以及子问题和原问题的关系,得到一个可能的(暂时未验证)利用子问题最优化得到原问题最优化的思路,然后假设原问题有个最优解X,则那么其子问题也一定是最优的,否则利用cut and paste就会得到矛盾,也就是可以构造更优的原问题解。
没有优化子结构的例子:(●ˇ∀ˇ●)
Question 4: How to design a DP algorithm?
5 Steps to solve a DP problem


Code
1 | # Generic Form of Dp Solution |
Summary
对于Dp其实核心就是如何把原问题抽象转换成subproblem DAG graph,graph的边其实就是状态转移关系。
Solution space 的一些思考,一般而言,绝大部分问题都能拆成指数级的决策树形式,从而挑选出最优解,但是这种方法根本没体现出问题的本质特征,信息利用率很低。Dp是通过利用所要求的属性(最优),将原问题的Solution space 看成Subproblem solution组成的Solution space,也就是DAG图。
所以对于DP的学习,重点就是在于学会如何建模,找状态表示(subprob),集合划分(construct DAG graph),状态转移方程就是DAG graph的连接关系,其实也就是会用y总的闫式DP分析法去解题。
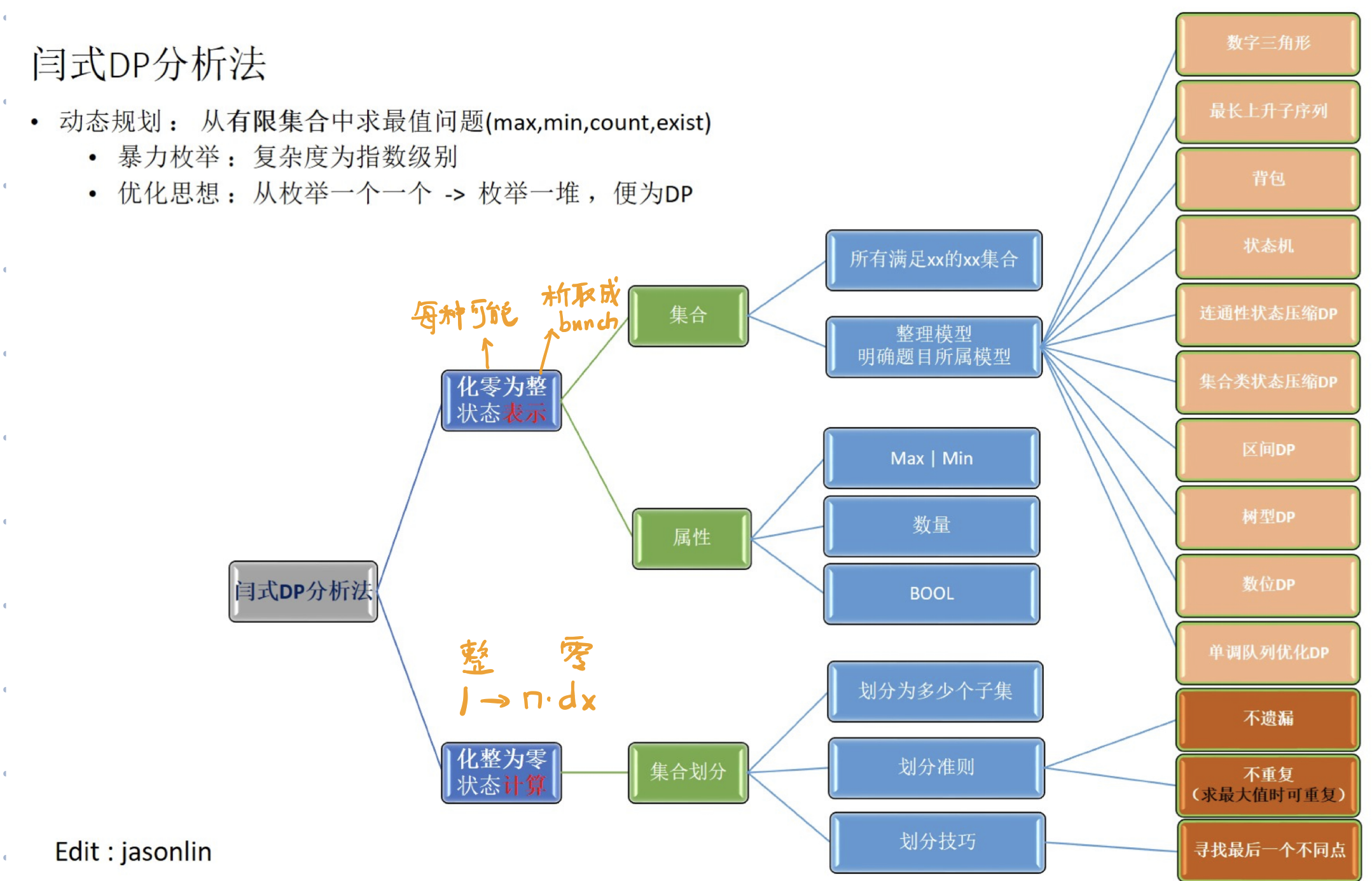
集合的状态表示其实就是子问题,而把原问题解析成子问题的DAG图,也就是集合划分干的事,通过只对时间代价很小的子问题求解,记忆结果,从而得到原问题的优化解。
下面就开始介绍具体问题了,也就是要结合具体问题学习状态表示,感受理解运用。
背包问题
0-1背包
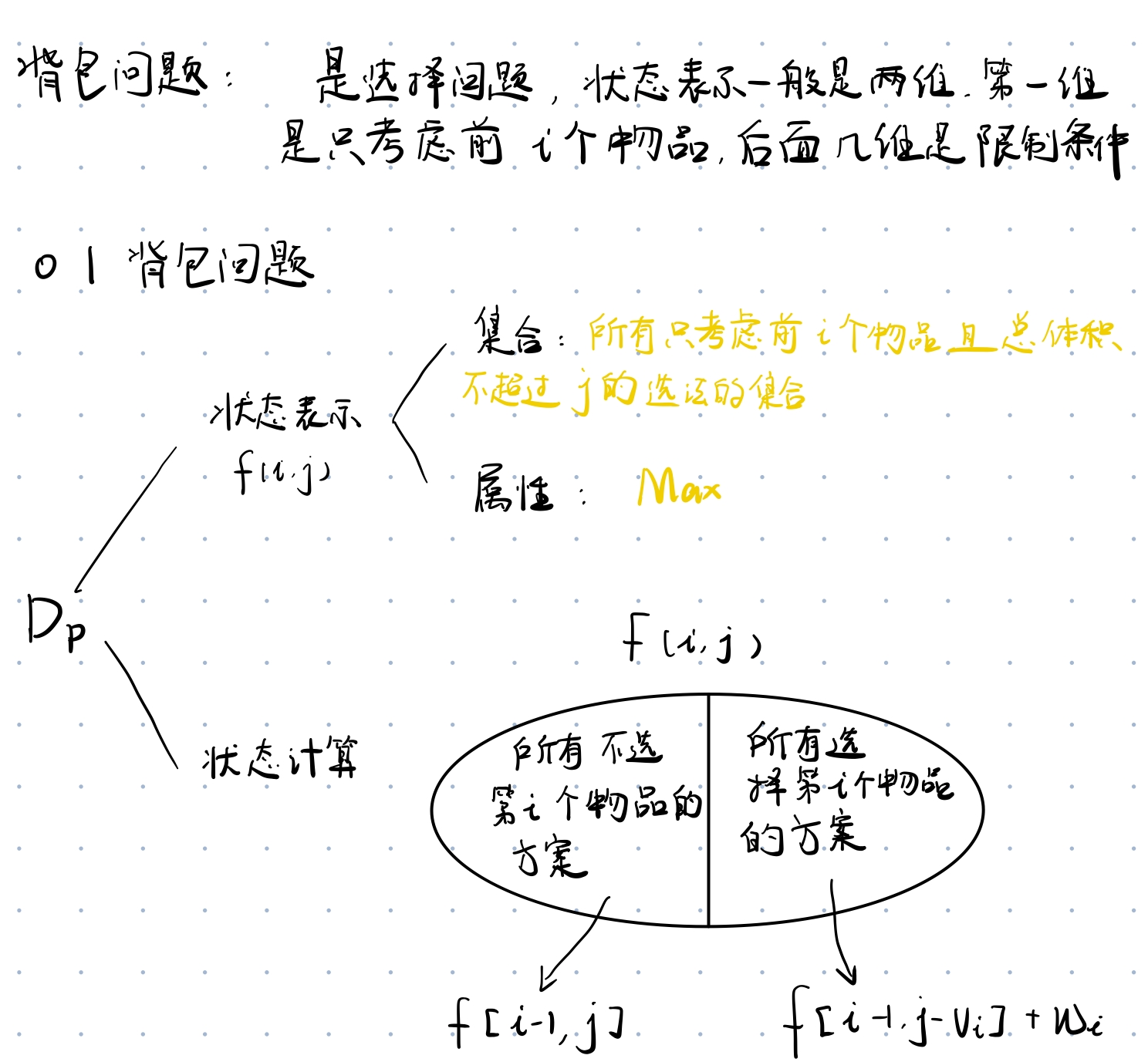
模板
完全背包
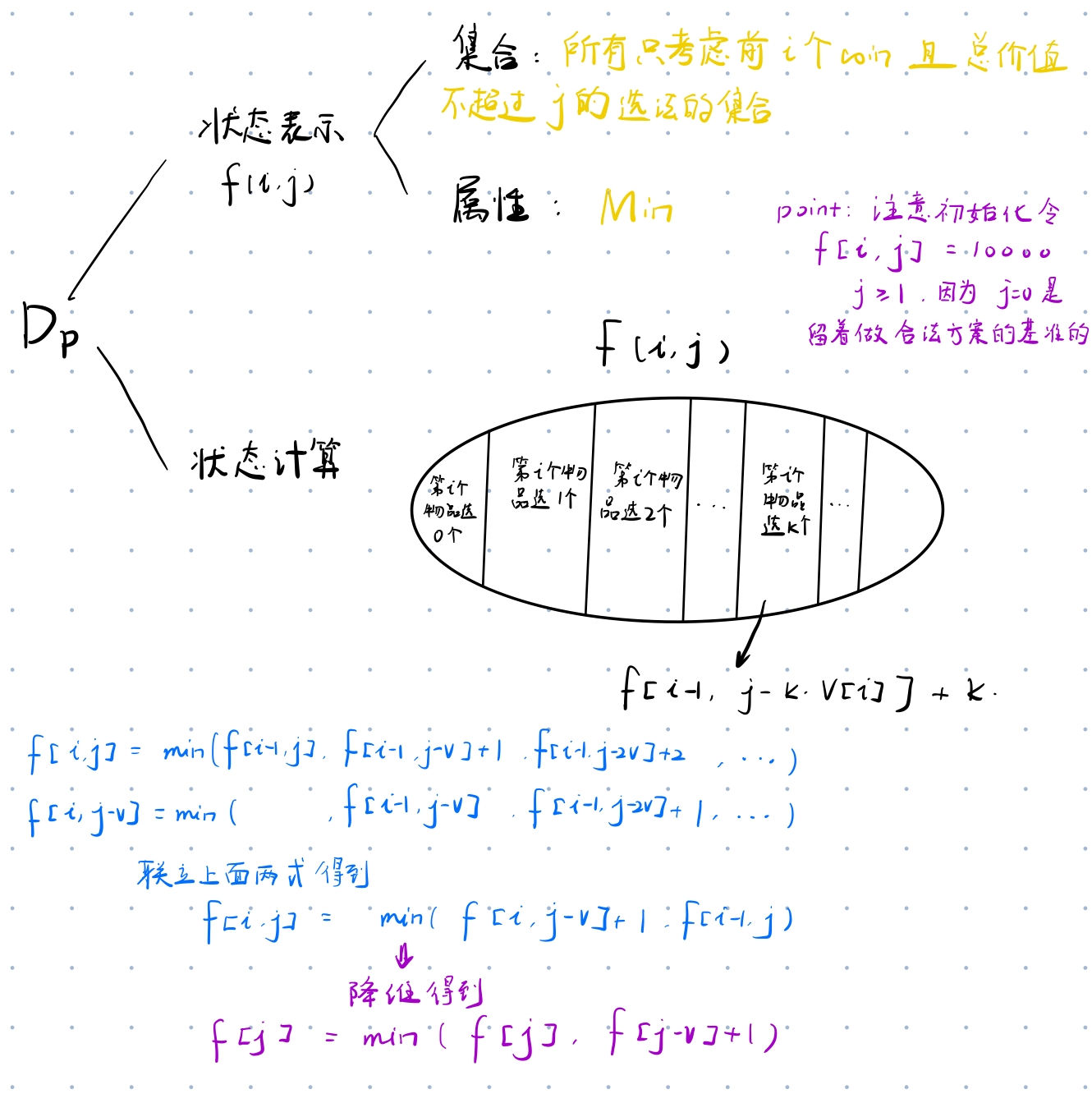
线性DP
题目区
区间DP
题目区
算法PPT里面的矩阵乘法和最优搜索二叉树
区间 DP 常用模版
所有的区间dp问题,第一维都是枚举区间长度,一般 len = 1 用来初始化,枚举从 len = 2 开始,第二维枚举起点 i (右端点 j 自动获得,j = i + len - 1)
1 | for (int i = 1; i <= n; i++) { |
关于整数的DP
900. 整数划分 - AcWing题库(计数DP)











