Classical Statistical Inference

窝工概率论这门课就很ba合理，课程安排很迷，因为马上考试，所以mit的课就没法全看了，姑且就sum一下课本的内容吧。

😃（笑脸继承张弛原大佬博客捏~ (￣▽￣)~*）

第六章数理统计的基本概念

其实这里讲的的几个Distribution是为了后面的的内容铺垫的（ep：置信区间的求解），由于这些Distribution是利用已知样本的一些特征量（说白了就是那些常见的，当然也要是符合良好性质的参数估计量）对参数进行替换，进而得到用这些特征量推得的新的分布（注意和原分布是不一样的，毕竟只是选取一部分随机的样本，方差肯定是更大）。

至于为啥要推导新分布，这里简要说明一下，一种比较naive的想法是，先用原分布推出所要求的置信区间表达式，或者其他的分布量，然后直接把对应的参数换成样本的特征量，得到答案。但是这种做法是有问题的，你所用于替换的特征量是一个random variable而不是constant，把原分布表达式的constant换成这个random variable可就不是原来的分布了，也就是说按照上面说的方法去求分布量是有误差的（这里说的误差指的是对于under the assumption of replacing parameter with 来说的）。而换成random variable以后的这个新的表达式也是可以计算分布函数的，那么就可以得到新的分布函数，然后利用这个新的分布函数去计算分布量，这样得到的结果就是准确的(under the assumption)

这章其实就是介绍常用的由特征量替换的random variable的分布，而且参数只保留了一个，其余都是统计量，通过查表和代数化简就可以去推出像置信区间之类的分布量。

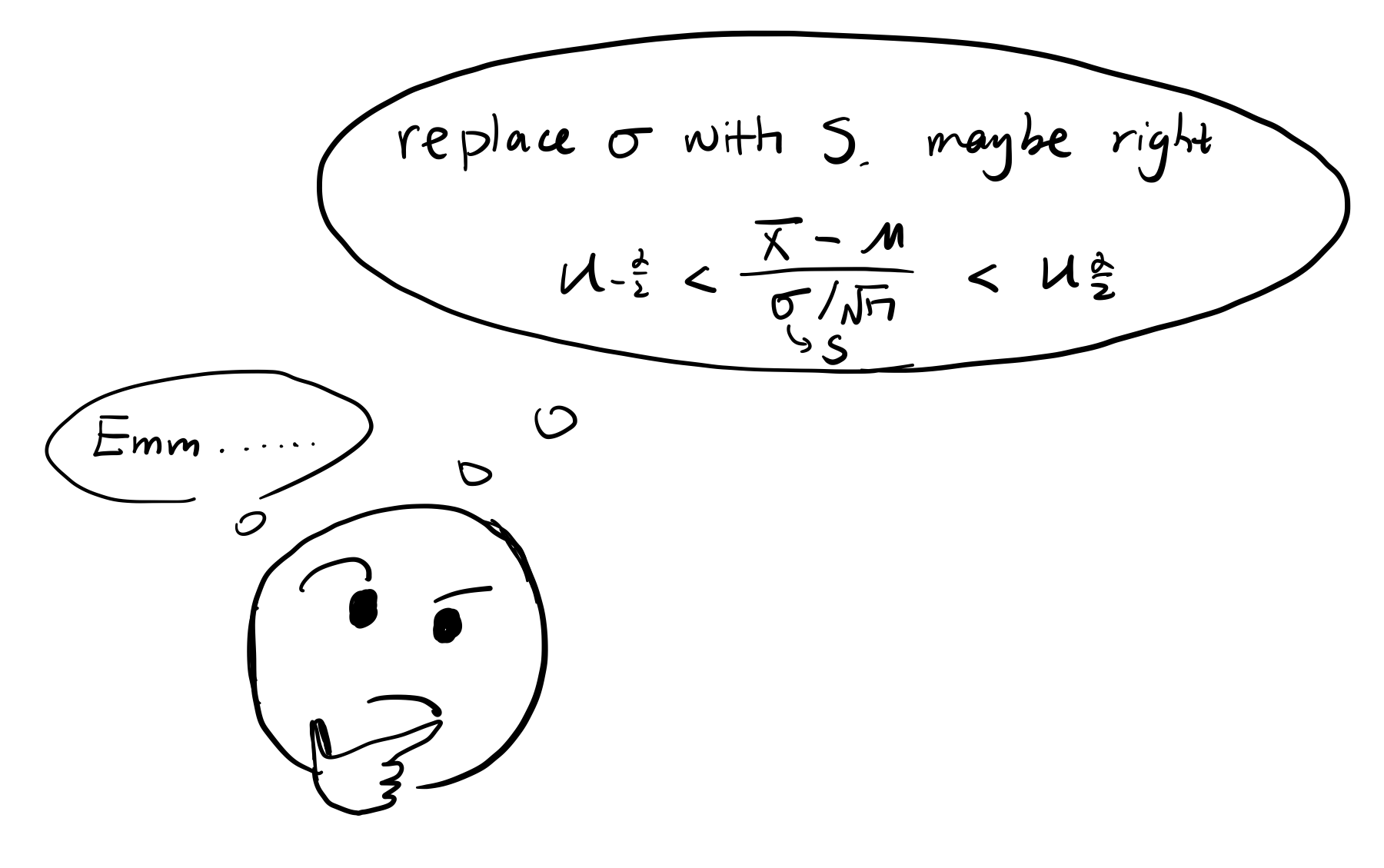
-Distribution

若，则，

卡方分布和指数分布的关系

设是来自总体的简单随机样本，服从参数为的指数分布，则

设是来自总体的一个简单随机样本，与分别为样本均值和样本方差，则

intuitive understanding 就是可以视为个Standard normal的平方和，也就是个的和，但是由于它们并不是独立的，因此没法用分布的可加性，具体而言其实这个和的自由度是的，服从。

具体的数学推导也是挺有意思的，见下面的链接：
样本方差的抽样分布_哔哩哔哩_bilibili

-Distribution

设相互独立，且，，则称随机变量

服从自由度为分布，记为。

设是来自总体的一个简单随机样本，与分别为样本均值和样本方差，则

已知，则

设和分别是来自总体和的两个简单随机样本，它们相互独立，则

其中

-Distribution

设随机变量相互独立，且，，则称随机变量

所服从的分布为第一自由度为，第二自由度为的分布，记为。

设和分别是来自总体和的两个简单随机样本，它们相互独立，则

有个叫三反公式的东西，在求置信区间之类的分布量的时候很有用

这个公式的证明捏就利用若则，以及分布的定义即可。

特殊的这个分布可以利用对称性来看，若，则，则有

题目

Point就是熟练各种变换即可

求样本分布

假设抽取容量为的简单随机样本，简单来说求样本分布就是求维独立同分布的随机变量的joint分布函数，求出相应的 or 。

推导、变换分布

服从正态分布：

or 这种就想到要化成标准正态分布，

看到这种就要想着化成分布。

遇到绝对值的这种把里面当成整体处理，要是这种形式，就把拆开，然后得到独立正态分布的线性组合，也是可以换成整体处理。

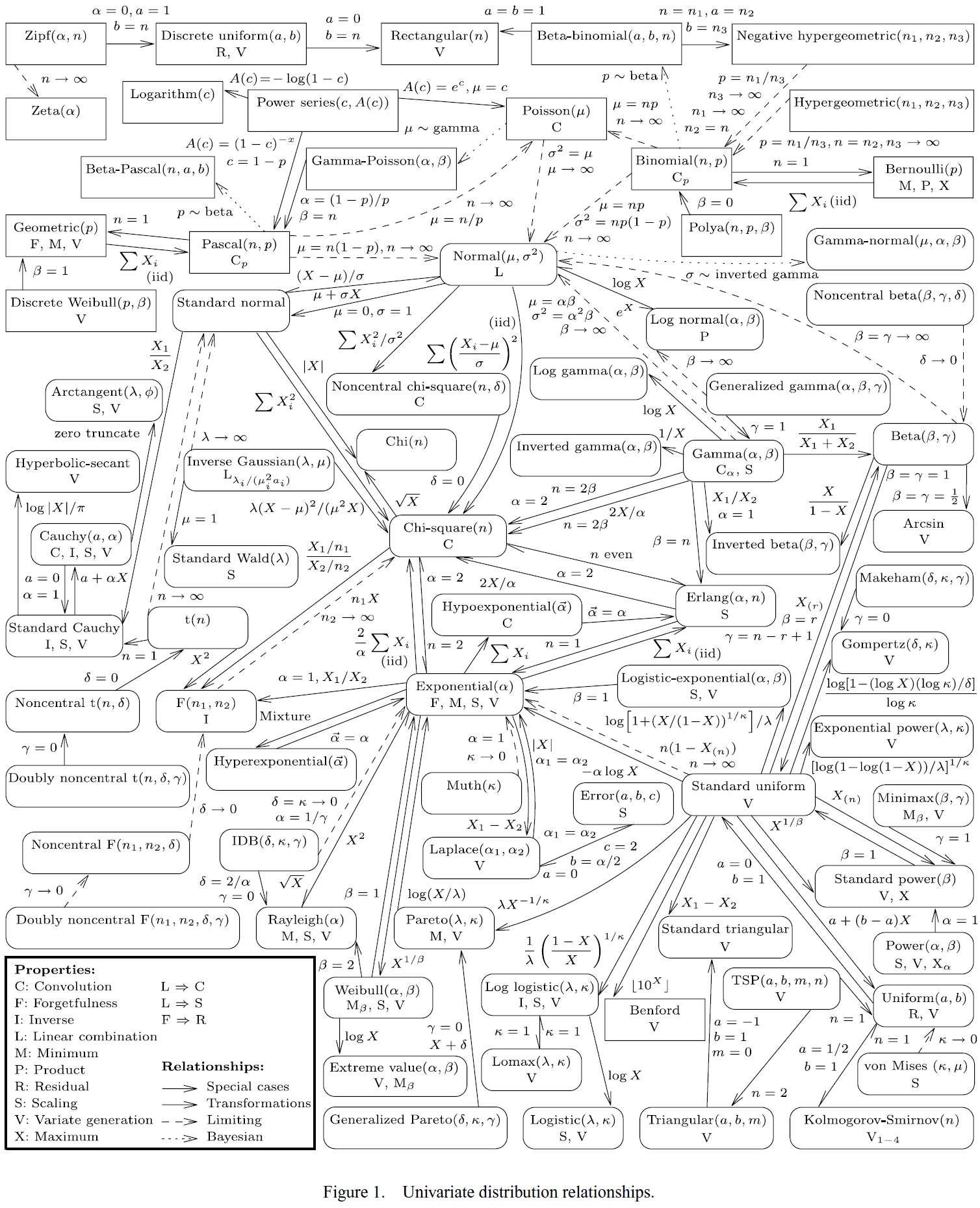
Absolutely great sum map of the univariate distribution relationships.

pdf

第七章参数估计

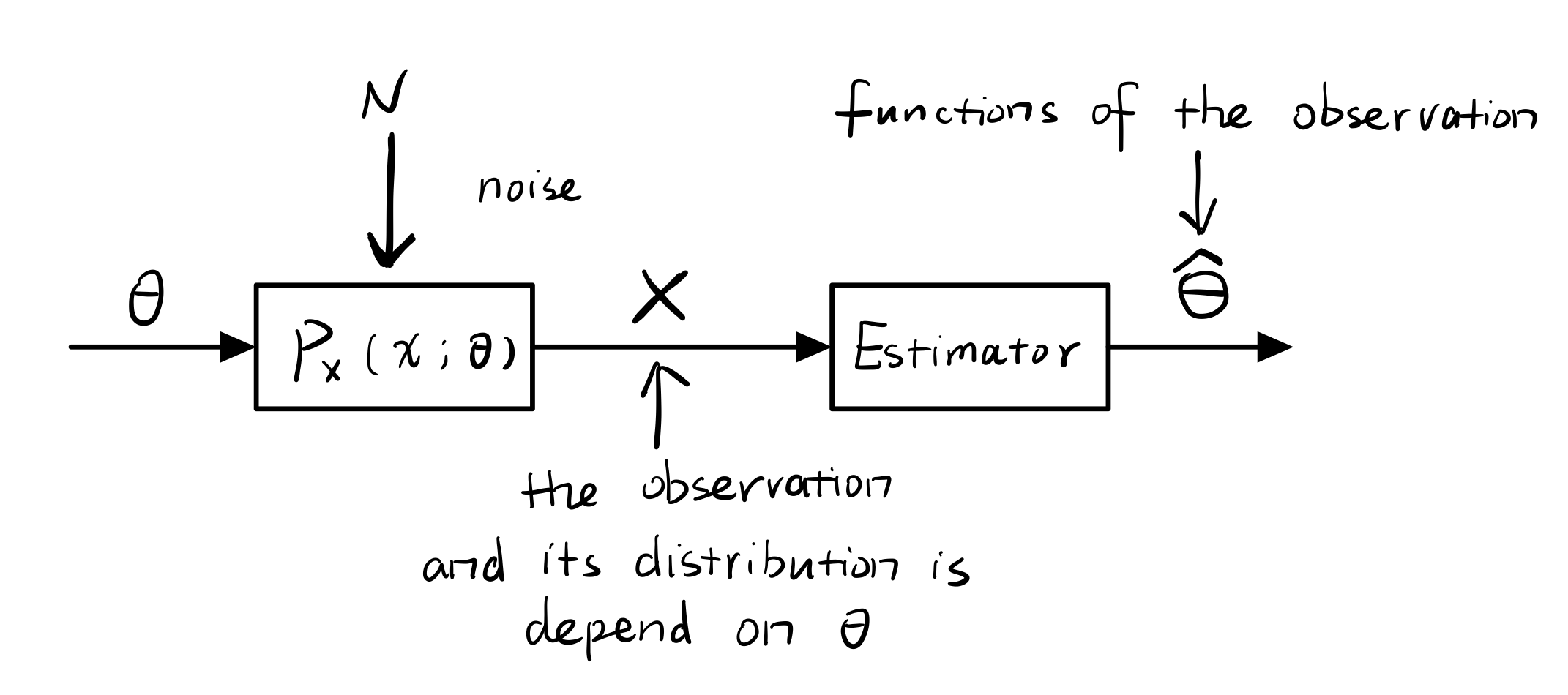
先把mit书上的 true parameter, observations ，estimator ，这三者的关系整明白，以及参数估计的标准(满足三个性质)和思路(MLE, Confidence interval)。

点估计

顾名思义，就是用一个值来估计参数的方法

矩估计法

样本的阶矩很自然是个用来近似parameter的function(而且确实是有比较良好的性质)，也就是用阶矩的组合来作为对进行估计，具体来说是把参数表示为总体矩的函数，，然后捏直接把用替换，也就是用表示了。可以这么做：

Suppose we have distribution function with parameter—>get expectation with the parameter—> considering the fact that converges to the mean , we can use to estimate the expectation—>plug into expectation, and present the parameter using

值得注意的是，这里是拿样本的阶矩直接带入，自由度啥的其实没考虑，因此可能是有偏的，具体来说，例如用矩估计法估计方差的时候，用的是样本的二阶中心矩，分母是，这其实是有偏的。

极大似然估计法(Maximum Likelihood Estimation)

The term “likelihood” needs to be interpreted properly. In particular, having observed the value of , is not the probability that the unknown parameter is equal to . Instead, it is the probability that the observed value can arise when the parameter is equal to . Thus, in maximizing the likelihood, we are asking the question:“What is the value of under which the observations we have seen are most likely to arise?”

利用比较朴素的思路，结合微积分计算得到作为参数估计的，其实也就是了。

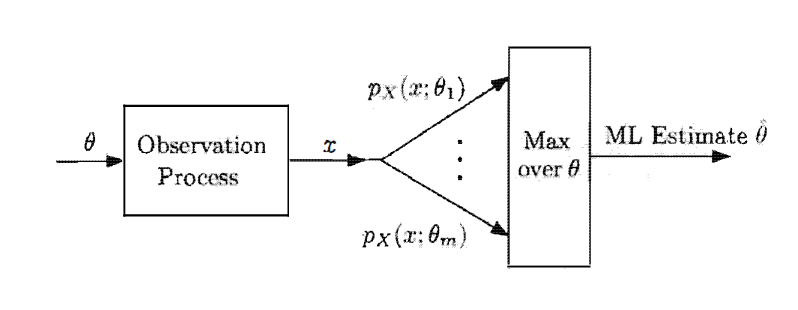
Here, the represents the candidate estimators, and we want to choose a that maximize the numerical function as our estimator .

似然函数的求法

具体来说，连续型的似然函数直接乘起来就🆗，毕竟是直接continuous numerical function，每个直接带入表达式即可求出对应概率。但是对于离散型，如果是countable infinite的情况，那么和连续型比较像，因为有个固定的表达式，直接带入得到概率；但是如果random variable 只能取finite个值，这时是要看样本的取值的，也就是要数取每个值的样本个数，然后乘起来。

有时候对似然函数难以求导，或者求导以后妹有极值点，这时候就要看定义了，其实本质就是让似然函数最大化，所以对于难以求导的情况，就看看几何意义或者其他角度来求最值，对于妹有极值点的情况就看参数本身有没有限制的范围，似然函数单调参数就取端点值。

具体来说，指数分布和均匀分布用极大似然估计去写的话就是这样。

鉴定估计量的标准

无偏性

无偏性指的是

样本均值都是总体均值的无偏估计(也好理解，毕竟自由度是n)，但是样本二阶中心矩(方差)不是总体方差的无偏估计(样本方差的话其实自由度是n-1了)。

实际应用中无偏估计的意义可以通过大数定理体现(大数定理表明实际的多次测量的sample mean是convergence to expectation)，也就是反复实验计算出个估计值，然后由是converge to real parameter 就能得到十分近似的估计。

所以捏，具有无偏性的估计量是有很好的实际意义的，但是只能保证在很大的时候是十分近似的，对于实际有时候取得不是很大，这时候就要考虑在无偏估计中选取方差较小的，保证实际不是很大也可以得到较好的估计。

注意是无偏估计，但是捏，却不一定是的无偏估计，原因是，把带进去即可。

有效性

有效性就是在无偏估计中选方差较小的。

zxr的评价是，多练练求方差捏。

相合性

相合性说的是估计的参数是依概率收敛于的，也就是$ \lim_{n\to \infty} P(|\hat \Theta_n-\theta|\geq \epsilon)=0 $$,\ \ \forall \epsilon >0$

常用的方法有利用，不等式，以及从pdf直接求这个区间概率然后取极限。

无偏性其实某种意义上暗示了相合性，也就是在取得非常大的时候，由大数定理就可以得到收敛的性质，但是无偏性是可以不体现相合性的，比如用很小的一些样本作为估计，而相合性只是在极限情况的性质，一般是体现不出相合的。

以正态分布均值为待估计参数，

无偏不相合：，虽然无偏，但是你只用一个，就算有无数个样本也还是用一个，不概率收敛。

相合不无偏：渐进无偏，方差收敛0，相合。

无偏相合：样本均值。

一般矩估计，MLE随便构造都是相合的，因为用了全部数据，因此相合性是很弱的一个性质。上面构造的无偏不相合就纯粹是构造的。

ps:值得注意的是，在证明对于的无偏性和相合性的时候，都用到了这个化简的等式。

区间估计

Besides the numerical value provided by an estimate, we are often interested in constructing a so-called confidence interval. A confidence interval for a scalar unknown parameter is an interval whose endpoint and bracket with a high probability.

Note that, similar to estimators, and , are functions of the observations, and hence random variables whose distributions depend on . And we call a confidence interval.

There’s also one point needed to notice, we cannot say that lies in the confidence interval with probability , because the latter statement does not involve any random variables; after all, in the classical approach, is a constant. Instead, the random entity in the phrase “the true parameter lies in the confidence interval” is the confidence interval, not the parameter.

In fact, we can use the distribution in Chapter 6 to derive the confidence interval, but how to interpret it? We first use the distribution to find a interval in which the probability of lying is at least , that is . We can view this differently, or to say, the probability of this inequality to be correct is , and we can just do some algebra to let take ’s position, to get another inequality but with the same probability $ [\hat \Theta^- \leq \theta \leq \hat \Theta^+]$ .