近世代数小记
基本构思一下具体的结构:每节内容的提炼,习题部分,big picture(各部分概念间的联系和逻辑架构)
复习思路:1.形成系统,也就是每一章讲了什么内容,每个具体的小节里有什么内容,都要很清楚(Tree Based Thinking)
2.对于每一节的内容,要有对应的题目支撑,也就是对应每节,涉及到某个概念时会有什么样的思路或trick(Network Based Thinking)
引言:数是我们研究数学最基本的对象,数的最基本运算是±*/,但是,数并不是我们研究数学的唯一对象,而且我们所遇到的许多运算也不全是数的普通加减乘除,例如向量、力以及多项式、函数、矩阵和线性变换等,它们虽然都不是数,但却也可以类似于数那样来进行运算,特别是。尽管这些研究对象千差万别,各有自己的特性,但是从运算的角度看却有着很多共同的性质,比如说n次单位根乘积,mod n运算,以及三角形的旋转翻转。于是,从一般的集合出发,研究各种运算的种种性质,就具有非常重要的意义。
集合和其上的代数运算形成代数系统,近世代数就是研究这些代数系统的学科,通过提炼不同具体的集合和具体的运算的本质,研究各种抽象代数系统间的关系和性质。抽象体现在两个方面:集合是抽象的,运算是抽象的,因此近世代数也称为抽象代数。
由于代数系统中运算的个数以及对运算所要求的附加条件的不同,从而产生了各种各样的不同的代数系统,这就形成了近世代数中各个不同的分支,其中最基本、最重要的分支是群、环、域。
我们知道,数、多项式和矩阵的出现是为了刻画一些物理量和几何量,例如长度、面积、速度、物理定律、空间中点的位置、平面的运动和几何变换等,它们的表现能力是很强的,使用数、多项式和矩阵足以刻画我们遇到的许多物理量和几何量。然而当人们企图刻画对称性——无论是物理现象中,还是数学世界中(尤其是几何图形中)的对称性时,都无法用单个的数,多项式或矩阵去刻画,为了刻画对称这一概念,人们发现了群,现在我们知道,群是研究对称性的强力工具,物理、几何、数学中对称这一概念的特殊重要性,使群称为近代数学极为重要深刻的概念。
Big Picture
群的组成分析
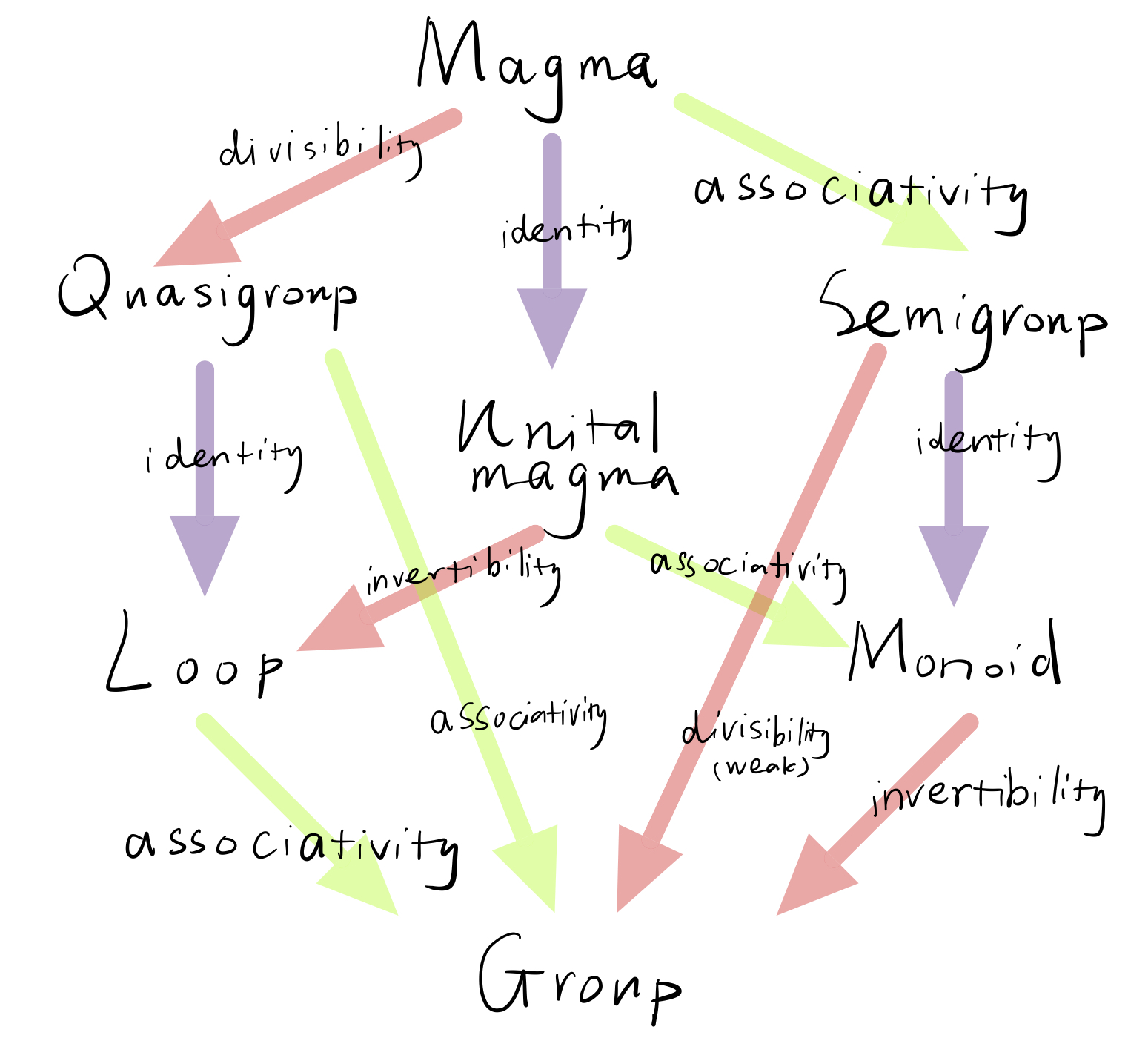
ps: Wiki里面的定义不同情况有些不一样,这里是按照书上定义和我自己理解的定义画的图
几个概念的辨析:cancellation,divisibility,invertibility
Divisibility does not imply invertibility, so they are distinct. One can have divisibility without an identity element; one needs both for invertibility. Note: a left inverse and a right inverse might not be the same, but invertibility does not demand this.
In this context, divisiblility is as in a quasigroup means, for every pair and
in the set, both existence and uniqueness of
and
that solve
and
. Not a great word. And not the most authoritative reference, but it gives several references. It is clear that quasigroup need not have an identity element, and hence need not support invertibility.
A better way to think about it is in terms of the translation maps and $R_a:M→M;x↦x⋅a $ for all
. In a division magma, these are all surjective. In a cancellative magma, they are injective. In a quasigroup, they are bijective.
对$\forall b \in M $,满射是说总存在一个x使ax=b
单射是说一一对应,如果则
(也算是填了个坑捏,消去律不一定是靠逆元,本质是一一映射的关系)
quasigroup可以理解为divisibility(弱化)+cancellation,也就是一般意义上的divisibility
但是如果是有限群的话,有限且相等(定理一),其实这三者就都是等价的了,都是双射,这也是为什么有限半群到群,只要满足最弱的消去律就行的原因。
注意:invertibility在不同群定义不一样,Wiki上的图很怪就是这个原因,这里理解为divisibility+identity
群的intuitive理解
循环群是转圈圈,像n次单位根群一样。
对称群是所有对称变换(转圈圈,翻转等)关于变换乘法的群,元素可表示为轮换的形式,表面上看起来置换好像和几何的这种对称变换没啥关系,实际上可以画画图就知道了,把顶点标上数字,任何对称的几何变换都对应着一个置换,以三角形的转圈和翻转为例,根据实施的变换(or最后的状态),可以得到这样的群,
是转圈,
是翻转,可以将三角形三个顶点按逆时针标号为
,其实这就得到了
,也就是三元对称群,本质上和对称变换群是一样的。如果把所有转圈的状态(k阶群的话,就是所有k轮换)提取出来,也就得到了一个循环子群。
研究思想
在近世代数,或者数学研究中,比较通用的思维是压缩条件,也就是尽量变成紧的性质。
比如说,循环群中提到的,生成系是群
中由子集
生成的子群,它是表示
中包含
的一切子群的交,是个紧的概念,但是
不一定为紧的,当
也为紧的时候,就引出了生成元的概念,一个元素生成群。
还有研究群之间相似性关系的时候,先是考虑同态满射,但是满射不是紧的,就想要对
中的元素进行聚类划分,使一个元素对应一个划分的类,这样就可以形成双射,进而是同构的,那么怎么划分集合呢,可以考虑用陪集对群中的元素进行partition,也就是陪集分解,但是一般地,这些划分(陪集)间只是商集,彼此间并无联系,但是这样在映射的时候就无法保证结构的维持,因此要构建商群,让这些商集形成群,考虑陪集的乘法,要想使运算封闭,就涉及到交换的性质,而这自然也就牵扯出正规子群的定义,进而到最后群同态基本定理,用
关于
的商群实现了最后的同构双射。
将上述推理推广,对于中包含
的正规子群
来说,其生成的商群其实也是可以和
中的
形成的商。群建立同构关系,详细可以看第三章的图。
特殊群记录
n次单位根群,也是n次有限交换群
若群的每个元素都满足方程
,则
为交换群,若
的阶大于2,则
必含有4阶子群。
8阶有限非交换群or四元数群
阶小于等于7的群的结构:
1阶群,单位元作成的群
2,3,5,7阶群为素数阶群,一定是循环群。
4阶群在同构的意义上只有两种(从也能看出):若不是循环群,则一定与
四元群同构。
四元群的形式
,运算为
这里需要注意的元素一定是要2阶偶置换才行,而与其同构的群(其余的
四元群)元素可以不是偶置换,这说明了,同构仅仅是代数性质上的相同,而对于元素本身的性质是无法迁移的。
6阶群在同构意义上只有两种:6阶循环群和对称群
四元数群的真子群只有4个:
为素数
若$p< q pq
G
q$阶子群。
若阶群
为交换群,则
必为循环群。
阶有限交换群有
阶元,从而有
阶子群。
证明技巧
证明是群的时候,先找到单位元,再去推逆元:半群到群的证明,变换群到双射变换群,环到除环
陪集相等的那个性质常用在证明单射(左右陪集双射,群同态基本定理)
从像集的性质反映原像的性质(同态映射那块证明)
课本内容提炼
第一章 基本概念
集合
- 定义(描述性定义) and 表示方法:列举法、描述法、Venn图法
- 性质:确定性、互异性、无序性
- 集合间关系 and 集合运算
- 运算律:幂等性、交换律、结合律、分配律、
定律
- 常用集合:子集,真子集,幂集,交集,并集,差集,余集
证明常用手段:$A=B \iff A \subseteq B \ B \subseteq A$
ps:别忘了
映射与变换
以下讨论默认映射是
映射的定义
- 2个point :
中每个元素,
中唯一确定元素与之对应。
- 可用于判断是否为映射
证明是映射的流程:
,要证明该法则为映射,则要对于
有
映射的相等判断
- P6 定理3
注意:若是
的双射,则
和
不相等,因为前者是
上的恒等映射
,而后者是
上的恒等映射
映射的种类
-
满射:focus on
中元素
为满射充要条件为
-
单射:focus on
中元素
为单射充要条件为
-
双射:一一对应,可由此定义逆映射
是双射的充要条件为
既是满射又是单射
之间可以建立双射充要条件为
映射种类的充要条件在证明中用的很多,ep: P6 定理1
定理一给出了相等情况下,满射和单射之间的关系。
逆像的概念
中所有元素在
全体逆像作成的集合称为
在
下的逆像,表示为
,它是
的一个子集,甚至可能是一个空集。
由此引出了结论(详见P5的图,其实就是不一定是满射导致的):
前者当是单射时等号可以成立(注意不是’等号成立说明是单射‘),后者是当
是满射时等号可以成立。
详见章末习题第七题
映射的合成
- 类似于链式法则,详见P6 定义3
注意是自右向左乘。
和
分别是
和
的映射
- 若
和
是单射,则
是单射
- 若
和
是满射,则
是满射
- 若
是单射,则
是单射
- 若
是满射,则
是满射
详见课后习题第九题
变换
变换是集合到自身的映射,也就是一种特殊的映射,由映射种类可同样定义满射变换、单射变换、双射变换。
代数运算
代数运算的定义
- 定义:使
中任意两个有次序的元素,在
中有唯一确定元素对应的法则。
- 也就是笛卡尔积到单个元素的映射
- 笛卡尔积的所有组合都能取到,而且结果是封闭的
可用于判断是否为代数运算。
变换的运算
表示
全体变换作成的集合,变换的乘法是
的一个代数运算
全体双射变换集合,变换的乘法也是其上的一个代数运算
运算的个数和变换的个数
上运算的个数:
的值:
的值:
permutation
运算律
结合律满足的话就可以任意加括号
交换律满足只是说明了两个元素间的运算可交换,多个元素不一定可交换
和
如果相等,则说明
等于
,也就是有了个加括号的性质,但是一般地,这是不满足的
同时满足结合律和交换律则可以任意加括号和交换
分配律一定要注意是哪个对哪个的分配,结果是不一样的
$\circ \oplus
\oplus
\circ$满足左分配律 是不一样的
同态与同构
概念定义理解
两个代数系统间的映射,不仅仅考虑元素间的对应关系,还要考虑运算性质的对应。
本质的理解就是,不仅要把元素映射,还要把元素间的映射映射了,一个代数系统不是毫无联系元素组成的集合,这些元素间是有映射关系的,也就是代数运算,如果想考察两个代数系统的similarity,那就必然要考虑这种内部的联系。
同态映射:保持运算的映射
自同态:M到自身的同态映射,本质是个映射
自同构:M到自身的同构映射
值得注意的是,对自同态/构映射而言,代数运算只有一个(两个的话也是相当于两个代数系统了=_=),或者可以理解为两个代数系统都是
,只要提供一个
符合条件的变换就行。
同态:描述代数系统间的性质,两个代数系统间存在同态满射就称为同态
同构:描述代数系统间的性质,两个代数系统存在同态双射(同构映射)就称为同构
同态下的运算律
若代数系统
则当满足交换律or结合律时,
也对应满足,但是反过来不一定成立,也就是
满足交换律or结合律,
不一定满足。
因为同态只是满射,考虑特殊情况只有1个元素很容易构造反例。
分配律而言,是两个代数系统中分别有两个代数运算,,其中一个对另一个满足分配律,ep:
对
满足左分配律(
),然后映射以后的结构也保持相同的性质。
等价关系与集合的分类
关系是对笛卡尔积的划分
等价关系是一种特殊的关系,不仅仅是对于笛卡尔积的划分,还可以对集合进行划分
ep:群按子群
的左陪集分解:
第二章 群
群的定义和初步性质
群
非空集合有代数运算
,满足以下条件则称
对这个代数运算作成一个群:
- 满足结合律
- 存在元素
,对
每个元素都有
- 对
中每个元素,在
中都有
书上是按左单位元和左逆元定义的,都是等价的
单位元是对所有元素都成立的,逆元的定义其实是用到了单位元
如果群中元素还满足交换律,则称
为交换群
半群
只要满足结合律就是半群,有单位元的半群称为幺半群,也说明了满足结合律和有单位元对群的组成来说,其实是相对独立的两个条件。
从半群到群的充要条件是对这两个方程有解
可以先推出单位元的存在,然后自然得到相应元素的逆元。
ps:注意是两个方程条件都要满足,只满足一个方程条件是不够的,例如经典例子:
其实这两个条件是弱化的divisibility,没有加唯一解的原因是可以推出解是唯一的
如果是唯一解或是有限群的弱化divisibility(双射了,肯定唯一),相当于暗示了代数系统中有这种结构性质的存在,也就是,说白了就是像
这种每行每列元素都不重复,有这种性质而无结合律的群称为
,这种群不一定有单位元和逆元,下面例子说明

有限半群成为群只要满足两个消去律即可。其实是有限使消去律,divisibility这两个条件等价起来了。
群中元素的阶
定义
是群
中的一个元素,使
的最小正整数称为
的阶。如果这样的
不存在,则称
的阶为无限。
有限群中每个元素的阶皆为有限,无限群中元素的阶可能无限,也可能有限,甚至可能每个元素的阶都有限。
按元素阶是否有限分类
若群中每个元素的阶都有限,则称
为周期群,若
中除单位元
外其余元素的阶都是无限,则称
为无扭群,既不是周期群又不是无扭群则称为混合群。
元素阶的定理
元素的阶其实是表明了一种周期的性质,和循环群联系起来,就可以由单个元素生成群的子群了。
元素的阶为
的充要条件:
已知的阶是
,则
的幂次
的阶为:
由此可得到,在群中若,则
的阶是
,
若群中元素,
的阶分别为
,
,则当
且
时,有
,即
交换群的一个性质:
设是交换群,且
中所有元素有最大阶
,则
中每个元素的阶都是
的因数,从而群
中每个元素均满足方程
挖坑:元素的阶涉及到质数分解,数论的一些定理,
这些,到时候把题目刷完了回来总结一下
子群
定义及性质
定义:设是一个群,
是
的一个非空子集,如果
本身对
的乘法也作成一个群,则称
为群
的一个子群。
如果,则子群
的单位元就是群
的单位元,
中元素
在
中的逆元就是
在
中的逆元。
群的非空子集
作成子群的充要条件是:
也就是结合律+可逆
或者是:
对有限子集作成子群的充要条件仅为
对
的乘法封闭
ps:
中每个元素的阶都有限,也是仅仅满足结合律就可以成子群(课后习题2)
因为元素阶有限就隐含了可逆性
任何群都不能是两个真子群的并(反证法,拿陪集看也挺明显的)
中心元和群中心
定义:同中每个元素都可换的元素
,称为是群
的一个中心元
若中心元只有,则称
为无中心群,交换群显然每个元素都是中心元
群的全体中心元作成的集合
是
的一个子群,称为群
的中心
群是交换群当且仅当
集合的乘积
用集合乘积的形式代表元素乘积的集合,进而描述关于群的一些条件和性质:
一个群的两个子群的乘积一般不再是子群,但是若子群和
的乘积满足交换律:
注意:这并不是说
中任何元素与
中任何元素相乘时都可互换,只是说乘积得到的集合
和
是相等的。
循环群
定义
如果群可以由一个元素
生成,即
,则称
为由
生成的一个循环群,并称
为
的一个生成元。
性质
循环群是元素幂次组成的群,所以证明一些概念的时候经常会用到元素阶的一些性质。
同构意义上看,循环群只有两种,整数加群和n次单位根群。
阶群
是循环群$\iff $$n
G
n$的元素
易知循环群是交换群
生成元
阶循环群的元素是生成元
这个元素阶为
无限循环群有两个生成元,即
和
,
阶循环群有
个生成元。
其中为
函数
循环群除了生成元外的元素,就都是阶为因数的循环群的生成元了。
循环群子群
(1)循环群的子群仍为循环群
这里的证明用了点技巧,证明由幂次组成的群是循环群:
- 选择合适的
作为生成元(一般选取最小正幂),则
- 任取
,证明
(2)子群的阶的性质
无限循环群有无限多个子群;当
为
阶循环群时,对
的每个正因数
,
有且只有一个
阶子群,这个子群就是
这个性质可以这样理解,循环群为交换群,则元素的阶都是最高阶的因数,而循环群的子群是靠群内元素生成的,循环群子群仍为循环群,得出结论:循环群的子群是阶为因数的循环群
但是如何保证有且只有一个呢,这里可以用直观的理解,把循环群看成复平面转圈圈,子群说明了是固定起点(单位元),然后是
因数说明是在更细化分
下的更大尺度划分,就肯定能转一圈,也可以理解为角度的划分,固定起点说明只可能是一种情况,就是有且只有一个。
阶循环群有且仅有
个子群
若,则
变换群
对称群
称集合的双射变换群
为
上的对称群,当
时,其上的对称群用
表示,并成为
元对称群
双射变换群
设是集合
的一个变换群,则
是双射变化群
中含有
的单(满)射变换
是双射变化群
包含恒等变换
非双射变换群
非双射变换群连单射和满射都不能包含,不存在含有只是单射or满射而不是双射的变换群,不是双射变换群的变换群就一定是非双射变换群。
设,则集合
的全体非双射变换关于变换的乘法不能作成群。
概念思考
既然只有双射变换群的单位元才是恒等变换,那非双射变换群的逆元和单位元如何解释,如何理解逆元的undo作用,和单位元的作用呢,明明单位元不是恒等的,这难道不怪怪的么。
这里的理解参见p38书上笔记,相当于是单位元把整体映射到新的空间下。
同构的性质
任何群都同一个(双射)变换群同构
通过构造映射
得到
任何阶有限群都与
元对称群
的一个子群同构。
对任何固定的正整数,互不同构的
阶群只有有限个。
置换群
轮换、对换表示置换
元对称群
的任意一个子群,都叫做一个
元置换群,简称置换群。
轮换(轮换),对换(
轮换),不相连轮换(无公共数码的轮换)
不相连轮换相乘时可以交换
每个(非轮换)置换都可以表示为不相连轮换之积,每个轮换都可以表示为对换之积,因此,每个置换都可以表示为对换之积
轮换可以写为
对换之积
奇偶置换
每个置换相当于是一个排列,对换相当于交换元素,是会改变逆序数奇偶性的,因此,每个置换表示成对换的乘积时,其对换个数的奇偶性不变。
可以取对换,构造
元置换群的双射
相当于奇->偶,偶->奇,且前后奇偶相同,令为全体奇置换的集合,
为全体偶置换的集合,则
中全体偶置换作成一个
阶的子群,记为
,称为
元交错群。
元置换及其逆具有相同奇偶性,因为
总是恒等变换,也就是偶置换,所以两者奇偶性相同。
置换的阶
奇偶看的是能拆成的对换的个数,而阶是指幂次以后等于
的性质,两者不同。
轮换的阶为
,不相连轮换乘积的阶为各因子的阶的最小公倍数。
阶数和置换的个数并无太大关系。
奇置换的阶只能是偶数
偶置换的阶可能是奇数,也可能是偶数
ep:阶数前者为偶,后者为奇
奇阶的置换一定是偶置换

化简置换的两个方法
- 画串线
- 图示法
详见书上
类似于线性变换的置换性质
陪集、指数和 定理
定理
定义
设是
的一个子群,
,则称群
的子集
为群关于子群
的一个左陪集。右陪集定义同理。
左右陪集一般不相等,ep: 的子群
{(1),(12)}关于(13)的左右陪集就不相等。
陪集的乘积一般不是陪集。
陪集的性质
,即
和
同在一个左陪集中
- 若
,则
这几条性质利用到拉格朗日定理证明的直观理解

群关于子群
的左陪集分解
其中称为
关于
的一个左陪集代表系。
左陪集和右陪集的联系
设是群
的一个子群,又令
则在与
之间存在一个双射。
在与
建立如下映射(陪集到陪集的逆):
可以证明这个映射及其逆映射都是单射。(若则
,利用了这两个表示的充要条件来证明)
是一个左陪集,则
也是一个右陪集,是与
互异且能划分
的,但是
不一定能和
形成一一对应,也就是会出现这样的情况,
中元素
,
但是
。
可以得到左右陪集代表系中的元素是互逆的关系:互异是不同的左陪集则
互异是不同的右陪集。
阶数
群中关于子群
的互异的左(或右)陪集的个数,叫做
在
里的指数。
对于阶数的讨论,也就是群的阶数,子群的阶数,元素的阶数的关系
群和子群的阶数是因数关系,设是有限群
的一个子群,则
而借助单个元素生成的循环群,可以得到群阶数和元素阶数的关系,也就是有限群中每个元素的阶都整除群的阶。
子群and阶数
设,
是群
的两个有限子群,则
利用是子群,然后将
左陪集分解了,再利用
进行化简。
ps:和第二同构定理还有些联系
设,
是两个素数且
,则
阶群
最多有一个
阶子群。
利用上面的定理可证
ps:其实是有且仅有一个
阶子群,
阶子群可以有很多
群在集合上的作用
(挖坑)
第三章 正规子群和群的同态与同构
群同构与同态的简单性质
A homomorphism is a way to compare two groups for structural similarities, it’s a map between two groups which preserves the group structure in each group.
设是一个群,
是一个有代数运算的集合,如果
,则
也是一个群。
设是群
到群
的一个同构映射,其实同构映射就可以把代数结构映射了,直觉感觉来看的话,元素间的代数关系像是一种
,也就是一种像是虚线连接起来的关系。
可以得出,的单位元的像就是
的单位元,
的元素
的逆元的像就是
像的逆元。对于含有群结构的集合,也就是子群,这种结构映射的性质体现的很明显:
- 当
时,有
,且
;
- 当
时,有
,且在
下诱导出
到
的一个同态映射;
群到群
的同态映射
是单射的充要条件是,群
的单位元
的逆像只有
。
如果不是单射(有多对一就行,不一定要求是满射),那么逆像就不只有了。
对于证明不是循环群的6阶群与同构,可以用书上的
定理和子群乘积的阶,也可以利用
则
有
阶元的结论。
正规子群和商群
定义
设是群
的一个子群,如果对
中每个元素
都有
则称是群
的一个正规子群。
若且
,则记为$N \lhd G $
平凡子群称为群
的平凡正规子群,
的其他正规子群,如果存在的话,称为
的非平凡正规子群。
设是群,
,则
or
性质
群的中心也是个正规子群
正规子群的正规子群不一定是原群的正规子群,也就是正规子群不具有传递性。
若,又
,则显然
是
的正规子群
同态满射下正规子群保持正规性,满射的原因是,正规这个性质 是对任意中元素都成立的,也就是映射的话是要覆盖所有的像,在这个基础上再保持代数结构,就会得到正规性了。
正规子群与一个子群的乘积是正规子群,两个正规子群的乘积是正规子群。
陪集的乘法是正规子群陪集上的代数运算,由此进一步提出商群的概念,也就是群的正规子群
的全体陪集对于陪集的乘法作成一个群,称为
关于
的商群,记为
。
商群的阶其实就是指数。
其实正规子群和中心群相比是弱的,前者只是集合相等的性质,而后者是所有元素对称的性质。
也就是和
交换群的性质
选交换群是因为其子群都是正规子群,通过元素生成的循环群也是正规子群,利用拉格朗日定理,商群的阶(指数)也就和元素的阶联系起来了。
定理:
设是一个
阶有限交换群,其中
是一个素数,则
有
阶元素,从而有
阶子群。
这里的证明是从商群中有阶元推出
中有
阶元。
推论:
阶交换群必为循环群。
 群和单群
群和单群
群
每个子群都是正规子群的非交换群。
四元数群就是一个群,而且是阶数最小的(8阶)。
素数阶群肯定都是交换群,不是群,4阶群也是交换群,6阶群也可以判断不是
群。
单群
阶大于1且只有平凡正规子群的群,称为单群。
的正规子群只有
有限交换群是单群的充要条件是为素数。
群同态基本定理
Big picture
首先理解的作用,首先它是个正规子群,所以可以形成商群。
被
划分,然后如果子群
包含
的话,说明子群也可以被
划分。其次,
中的元素
乘以
就会得到一个陪集,这个陪集的像(一个元素)就是
,而反过来,
的逆像也就是这个陪集(单射性)。
用数学语言来描述的话就是:设为
的子群,
是群
到群
的同态映射,
对于,$\exist c \in H\ s.t.\varphi(a^{-1}b) =\varphi© \ or \ \varphi(c^{-1}a^{-1}b) = \bar e
c^{-1}a^{-1}b \in Ker\varphi \sube H
a^{-1}b \in H
aH=bH$ .
然后群同态基本定理说的就是由划分的这些
陪集是和
中的元素一一对应的,然后引理,定理4也可利用这个直观的理解解释捏。
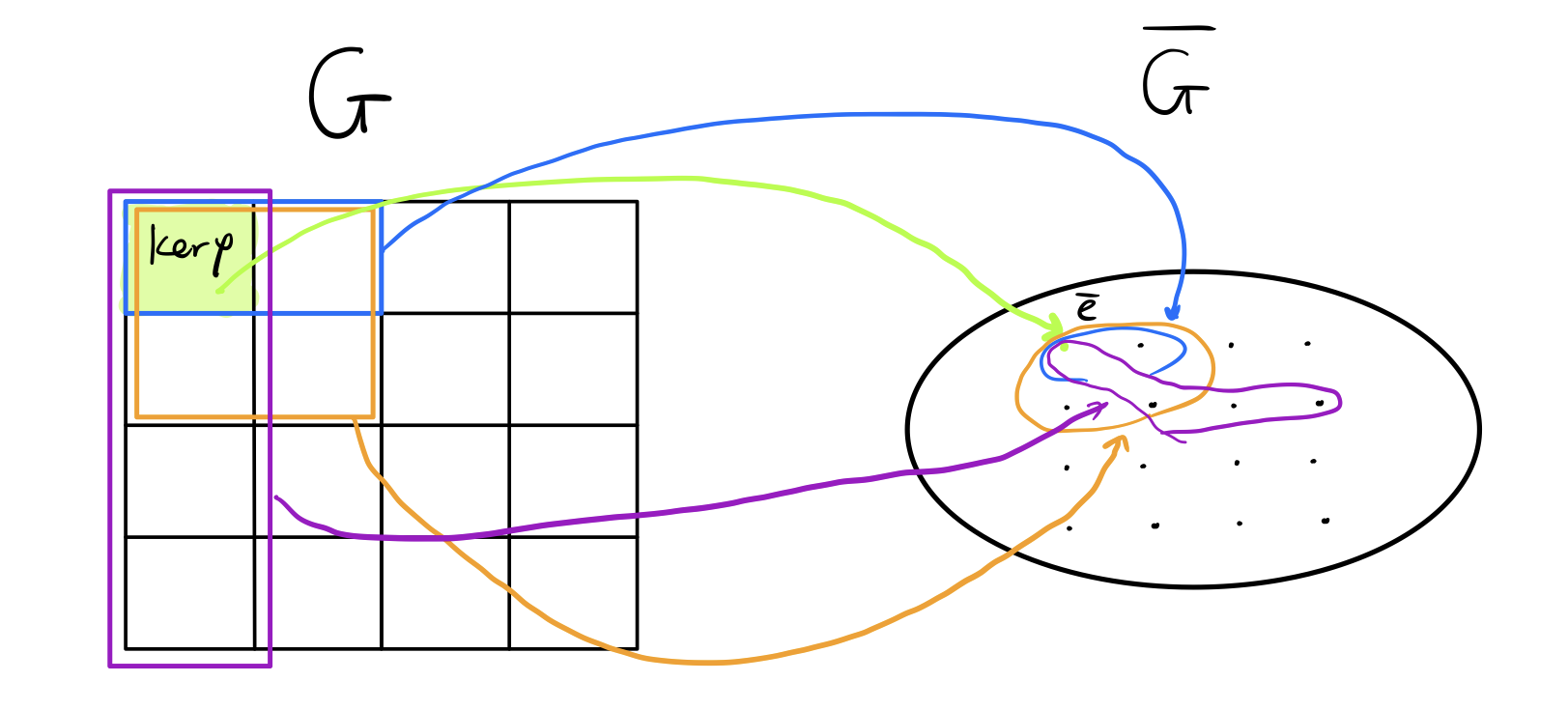
概念定义
设是群
的任一正规子群,则
任何群均与其商群同态。
称同态满射
为到商群
的自然同态。
设是群
到
的一个同态映射,
的单位元在
之下的所有逆像作成的集合,叫做
的核,记为
。
定理
设是群
到
的一个同态满射,则
,且
证明分为3个阶段,证明是映射,证明是满射,证明是单射。证明的point是借助进行过渡。
性质
同态满射下,循环群的同态像是循环群,生成元的像也是生成元。
也就是说,循环群的商群也是循环群。
子群的关系
群同态映射下,两个群子群间的关系:
设是群
到
的一个同态满射,核是
,则G的含
的所有子群与
的所有子群间可建立一个保持包含关系的双射。
群同构基本定理
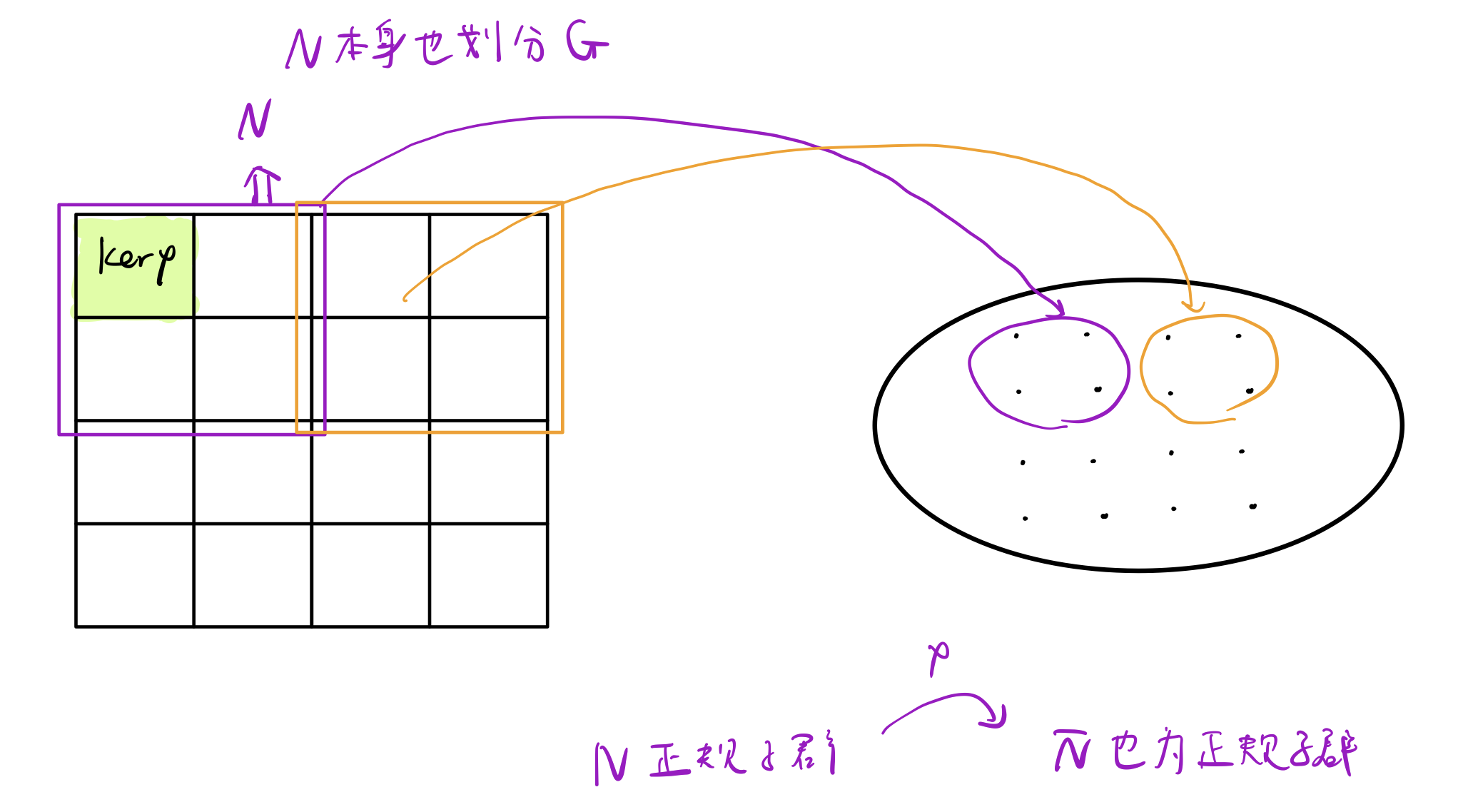
Big picture
群同态基本定理考虑的是陪集到元素的对应关系,而群同态则考虑从陪集到陪集的一一对应。为什么会想到这种性质呢,其实这相当于是对群同态基本定理的扩展,考虑包含的正规子群,那么像下图这样,
在更大尺度下被划分,而且对应的
中也是被划分为正规子群和陪集,不难发现,其实这可以形成一个同构,也就是
与
之间的由
形成的同构。
第二同构定理描述的是子群和正规子群,以及他们的乘积和交的关系。书上证明是用的的同态满射。
第三同构定理说明商群中子群的特征,也就是,商群中的子群仍为一种商群,而且商群之商群可以类似于普通分数那样约分。证明的时候注意唯一单射性和包含
的子群的像的表示。
群的自同构群
自同构群
设是有一个代数运算(叫做乘法)的代数系统,则
的全体自同构关于变换的乘法作成一个群,称为
的自同构群。
这里的元素是上的自同构映射,也就是
的同态双射。
如果是是群的话,就称为是群
的自同构群,记为
。
若$ \sigma \tau
M
\sigma \tau
M
\sigma^{-1}
\tau^{-1}
M$上的自同构。
自同构把单位元变成单位元,
无限循环群的自同构群是一个2阶循环群;阶循环群的自同构群是一个
阶群,其中
为欧拉函数。
证明:生成元的对应关系完全决定了群中其它元素的对应关系。因此,一个循环求有多少个生成元就有多少个自同构。例如,设是由
生成的循环群,则当
是小于
且与
互素的整数时,
也是
的生成元,即
。此时,令
,则有
,且
时,
,(如果
不是和
互素,则就不是双射)且
,即
是
的自同构。
涉及自同构群的一些结论(常借助内自同构群证明)
非交换群的自同构群不能是循环群。
无中心群的自同构群也是无中心群。
若群的自同构群是一个单位元群(即
只有恒等自同构),则
必为交换群且每个元素都满足方程
。
内自同构群
设是一个群,
,则
是
的一个自同构,称为
的一个内自同构。
的全体内自同构作成一个群,称为群
的内自同构群,记为
的正规子群就是对
的所有内自同构都不变的子群,因此正规子群也成为不变子群。
任何非交换单群必与其内自同构群
同构。
内自同构群和由中心群划分的商群是同构的:
设是群
的中心,则
特征子群和全特征子群
特征子群
对群的所有自同构都不变的子群
,亦即对
的任何自同构
都有
这样的子群称为的一个特征子群。
这里条件也可改为是
的特征子群当且仅当对
的每个自同构
都有
。
群的中心是一个特征子群。
特征子群一定是正规子群,反之不一定成立。
全特征子群
设是群
的一个子群,如果
对
的每个自同态映射都不变,即对
的每个自同态映射
都有
性质
虽然正规子群没有传递性,但是特征子群和全特征子群是具有传递性的,也就是特征子群的特征子群还是特征子群。
原因:对于上的全体自同构,对于其特征子群
来说也是其上的自同构,因此
的特征子群
还是特征子群。
则称为群
的一个全特征子群。
循环群的子群都是全特征子群。
 定理
定理
(挖坑)
第四章 环和域
环的定义
记号规定
交换群的代数运算叫做加法并用加号表示时,称为一个加群。
加群中的单位元用来表示,称为零元,元素
的逆元用
表示,并称为
的负元。
如果把简记为
,那么在加群中就有了一个减法,它是加法的逆运算。
乘群中通常的指数运算规则在加群中自然改为倍数(注意和环中乘法区分)规则:
,左边的
是数零,右边的
是零元。
,一共
个相加,
为正整数。
定义
设非空集合有两个代数运算,一个叫做加法(一般用
来表示),另一个叫做乘法,如果
-
对加法作成一个加群
-
对乘法满足结合律
-
乘法对加法满足左右分配律
其中为
中任意元素,则称
对这两个代数运算作成一个环。
常见的有:数域上全体
阶方阵集合和多项式集合(表示为
),分别称为数域
上的多项式环和
阶全矩阵环。
分类
如果对于乘法满足交换律,则称为交换环,否则称
为非交换环。
如果环只含有限个元素,则称
为有限环,否则称
为无限环。
有限环的元素个数称为
的阶,无限环的阶称为无限。环
的阶用
表示。
设是一个加群,再对
中任意元素
规定
,则
显然作成一个环,这种环称为零乘环。
乘法性质
环的单位元是对于乘法来说的,毕竟加法已经成群了。
如果环中有元素
,它对
中每个元素
都有
,则称
为环
的一个左单位元,右单位元同理,环
中既是左单位元又是右单位元的元素,叫做
的单位元。
如果环有单位元,则显然是唯一的,一般用
表示。
一个环可能既无左单位元,也无右单位元,例如偶数环(没有),也可能只有左单位元无右单位元,只有右单位元无左单位元。
乘法的运算规则:
,
是环的零元
,
- $(\sum_{i=1}^ma_i)(\sum_{j=1}^nb_j)=\sum_{i=1}^m\sum_{j=1}^na_ib_j $
子环
设是环
的一个非空子集,如果
对
的加法和乘法也作成一个环,则称
是
的子环,记为
。
值得注意的是,当有单位元时,
不一定有,当
有单位元时,
不一定有,即使两者都有单位元,也不一定相等。
环的零因子和特征
环的零因子
设是环
的一个元素 。如果在
中存在元素
使
,则称
为环
的一个左零因子。同样可以定义右零因子,左右零因子统称为零因子,只在有必要区分时才加左或右。
当无左零因子时,也无右零因子,因为若有了则说明
,这说明其实
也是左零因子。
既不是左零因子也不是右零因子的元素,称为正则元。
零因子和消去律
在无零因子的环中,关于乘法的消去律成立。若环无左(或右)零因子,则消去律成立;反之,若
中有一个消去律成立,则
无零因子,且另一个消去律也成立。
若环中有左单位元
,且无零因子,则
为环
的单位元。
环的特征
阶大于、有单位元且无零因子的交换环称为整环。
若环的元素(对加法)有最大阶
,则称
为环
的特征(或特征数)
若环的元素(对加法)无最大阶,则称
的特征是无限(或零)
有限环的特征必有限,无限环的特征可能有限可能无限。
考虑无零因子和有单位元的影响
无零因子环特征定理
一般来说,环中各元素阶(对加法)是不相等的,但是捏,对于无零因子环来说,确实是相等的。
设是一个无零因子环,且$|R|>1 $,则
中所有非零元素(对加法)的阶均相同
- 若
的特征有限,则必为素数
第一条是利用了乘法的消去律,以及乘法和加法的幂可换,第二条其实属于是结论,也就是:对于除单位元外元素阶数相同的群,这个阶数是素数或者无限。
有单位元环特征定理
若环有单位元,则单位元在加群
中的阶就是
的特征。
除环和域
设是一个环,如果
,又
有单位元且每个非零元都有逆元,则称
是一个除环。
可换除环称为域。
除环和域没有零因子。
ps:无零因子和没有逆元是不一样的,零因子一定不是可逆元。
考虑的性质:有限,单位元(零因子不考虑是因为俺们在讨论除环,有逆元的性质)
有限环性质
有限除环必为域。
阶大于的有限环若有非零元不是零因子,则必有单位元,且每个非零又非零因子的元素都是可逆元。
阶大于的有限环
若无零因子,则必为除环(域)。
除环充要条件
设是环且
,则
是除环当且仅当对
中任意元素
和
,方程
在中有解。
有单位元环性质
一个有单位元的环的全体可逆元对乘法也作成群。
设是一个有单位元的环,则
的可逆元也称为
的单位,
的全体可逆元作成的群,称为
的乘群或单位群,并用
或
表示。
习题
第一章
对于逆像中的元素,也就是这样形式的,处理方法是直接加
,得到
对于像中的元素,也就是形如这样的,处理方法是,
对于映射合成的套路是:
单射将内部的映射和元素结合处理,也就是
满射是对于任意的像中元素,都存在原像,ep:为满射,对
,于是
元素阶数
交换群中所有有限阶数元素作成一个子群。
若中除单位元
外其余元素阶都相同,则这个相同的阶不是无限就是一个素数。
在一个有限群里,阶数大于2的元素的个数一定是奇数;偶数阶群中阶等于2的元素的个数一定是奇数。
设群中元素
的阶是
,且
,证明:在
中存在元素
使
并且这样的元素是唯一的。
设是群,
,又
其中是两个整数,若
,则
设是群
中两个有限阶元素,且
则
循环群
阶无限和阶有限的处理差异,若,则在无限条件下,可以直接得到
,而在有限阶条件下是
的处理方法:
利用互质,结合
这个性质可得
,其中
是整数。
然后再,对于
,利用
设是群
的一个子群,且
,又
是
关于
的余集,则
循环群的证明套路
第三章
正规子群
为群
的正规子群,商群为
其实对于涉及商群的证明,只要关注陪集分解系数即可,因为是正规子群,性质太强了,满足交换律。
对于商群中元素和中元素的关系,
证明商群为交换群,主要考虑这个因子的存在。
设是群,
,证明:如果关于
的任意两个左陪集的乘积仍是一个左陪集,则
。
第四章
期末考梳理
也算是封顶大吉了o( ̄▽ ̄)ブ
作为深圳窝工第一届考近世代数的cs本科生,没有往年题目,没有考试范围和重点,嗯,让人感到着实蛋疼。复习全靠随缘,考试就用心对待就好了(会写的写好,不会写的尽量去写),可不能完全摆烂捏。
本节由一名cs羸弱在考试前一天下午赶工,希望考试顺利捏~( ̄▽ ̄)~*
后记:最后时间紧迫,这部分没写完了就是,考试比较容易,基本都是书上的证明U•ェ•*U
第一章
第一章的话看之前的笔记就行了,很精简而且全面,这里不再赘述。
第二章
第一节,群的定义和初步性质。
5个点:
- 群的定义
- 群的分类和常用群
- 单位元逆元左右相等且唯一
- 半群和幺半群的定义
- 半群and有限半群成群条件
第二节,群中的元素的阶。
3个点:
- 阶的定义
- 群按阶数的分类
- 有关阶的定理,有关交换群阶的定理
第三节,子群。





