上学期的笔记，图片很多没上传，有时间来弄

误差

固有误差：

  • 从实际问题抽象出的数学模型----模型误差
  • 通过测量得到模型中参数的值----观测误差

计算误差：(设计数值算法所需要关注的)

  • 求近似解----方法误差（截断误差）
  • 机器字长有限----舍入误差

绝对误差：(依赖量纲)

，其中为精确值，为的近似值。

表征测量值和精确值之间的差异的上限记为，称为绝对误差限。

工程上常记为

相对误差：(不依赖量纲)

，但是通常未知，估计，的相对误差上限定义为

这样代换是合理的，${e^\over x} {e^\over x^*}$反映的是同一数量级上的误差。

1.png

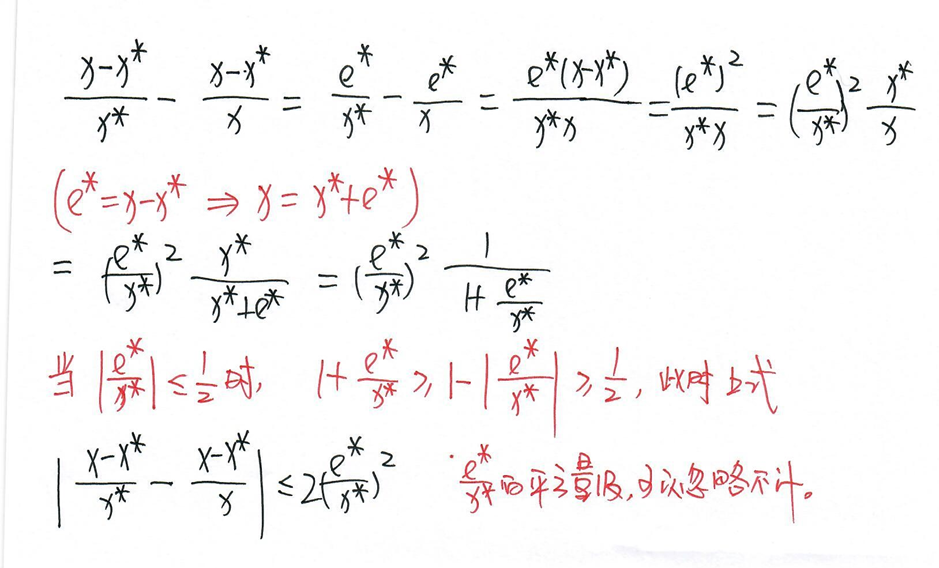
有效数字：

有效数字是用绝对误差界定义的，若的某一近似值的绝对误差界是某一位的半个单位(四舍五入规则)，则从这一位起直到左边第一个非零数字为止的所有数字都称为的有效数字。

这部分说人话就是这样的，真实数据按照四舍五入原则取得的小数就直接按照朴素的有效数字定义来看即可，比如，然后，正常按照四舍五入截取，然后这个有效数字的位数就是5位了，如果说不是按照四舍五入的原则，比如这里取的话，有效数字的计算按照如下进行

则称为位有效数字，精确到。

数值计算中应该注意的若干问题：

  • 防止有效数字的损失
    • 避免相近两数相减
    • 避免大数吃小数
  • 减少计算次数
  • 选用稳定的算

非线性方程和方程组的数值解法

二分法

A similar situation exists for discretization methods. The important parameter here for the convergence speed is not the iteration number k, but the number of grid points and grid spacing. In this case, the number of grid points n in a discretization process is inversely proportional to the grid spacing.

In this case, a sequence said to converge to L with order q if there exists a constant C such that

This is written as using big O notation.

比如二分法，其实误差的保证并不是靠迭代的数字保证的，而是靠区间的大小，也就是会出现前一次的误差其实是会比后一次小，但是区间在缩小，保证的误差界限也在缩小。

对于给定精度，可以估计二分法所需要的步数:

这里多提一嘴，这个步数实际在这个表达式里是用了，原因是这样的，实际上计算二分区间不算一步，只有更新节点才算一步。也就是说刚开始是第0步，就可以计算出二分区间的大小。

评价：

  • 简单、对只要求连续
  • 但是无法求复根和偶重根，收敛慢，对的值利用不够

不动点法

The intuition behind Fixed Point Iteration method: (Lipschitz continuous)

2.png

https://math.stackexchange.com/a/721497/980786

The geometric graph of FPI

3.png

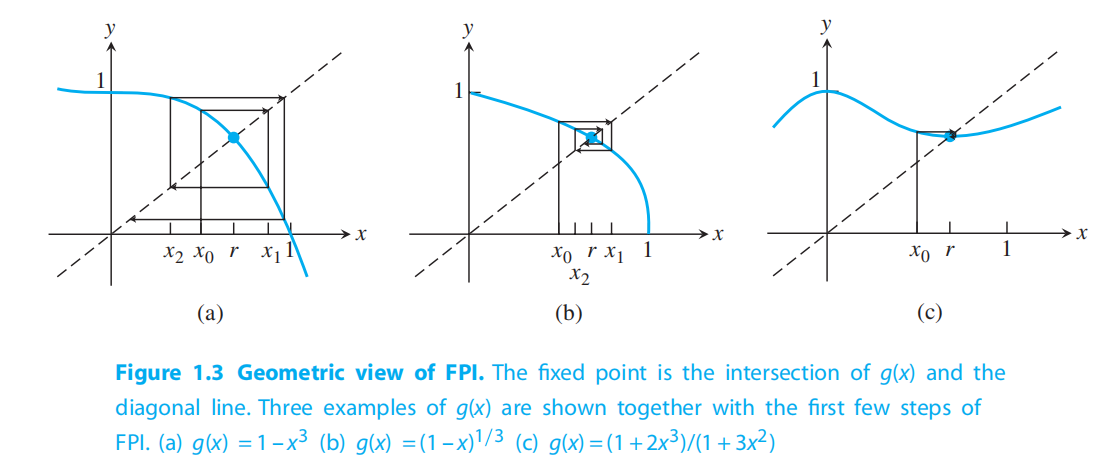
单点迭代法收敛性：

考虑方程，若

  1. 当时，；
  2. 使得对成立
    (这里条件换为Lipschitz continuous也可)

则任取，由得到的序列收敛于在上的唯一不动点，并且由误差估计式：

这个证明是用了绝对值不等式，$|x_{k+1} - x_k|\geq |\alpha - x_k| - |\alpha - x_{k+1}| \geq |\alpha - x_k| - L|\alpha - x_{k}| $

还有的放缩，以及的放缩(中值定理)

Here are definitions of linear convergence and locally convergent

6.png image-20220517100929628 5.png

单点迭代法的收敛阶：

4.png

已知在内仅有一个根，而当时，，试问如何将化为适合于迭代的形式。（P36，3）

转成反函数，因为不动点都是一样的，但是导数就变成倒数了，符合收敛性。

Newton迭代法

不妨先从intuitive的思考开始，求根问题的本质是什么，其实可以理解为给定一个函数，求处对应的取值，考虑连续且有足够阶导的情况，最naive的想法就是先在给定区间随便选取一点，再根据和一步一步"爬"到给定的高度，记录此时的值，这种思想其实和梯度下降有点类似，但是问题在于step size是很难合适的选取以保证收敛（机器学习里面倒是有套收敛的理论，但是和目前讨论的问题是不一样的，此外补充一下，Newton下山法就是这种思想）。一种解决方法是可以用迭代的思想确定下一步的位置，但是对于迭代的sequence是要满足收敛性的。此时我们可以先观察图形得到intuition然后再去细致数学证明。

对于及其扩展，intuition是在当前点去尽量拟合原函数，也就是取泰勒展开的的项，得到的多项式去求和 的交点，得到点继续迭代。

的资料：

https://www.youtube.com/watch?v=F9DFewL0mho

Newton迭代法的局部收敛性

牛顿迭代法是平方收敛的，

令，通过移项化简可得

lies between r and ，it converges to as does

7.png

Newton迭代法的非局部收敛

设在有根区间上二阶导数存在，且满足

  3. 不变号，
  4. 初值且使

则迭代序列收敛于在内的唯一根。

Newton迭代法的改进：

Newton法不足：

  1. 初值不能偏离根太大，否则可能不收敛
  2. 要计算导数值
  3. 重根问题会寄

(46条消息) Newton牛顿法（二）| 收敛性和收敛速度 +初值的选取方法_Sany 何灿的博客-CSDN博客_收敛速度怎么求

考虑到Newton迭代的形式本身就是一种特殊的FPI，所以就可以放弃二阶收敛的特性，进行改进，保证运算简化。

  • 简化Newton迭代法，就是把导数值换成了个常量，相当于说就是FPI的一种特殊形式应用，是一阶收敛。

  • 多点迭代法利用之前计算出的值来近似导数值，而不是像简单Newton法那样naive的替换，这样得到的局部收敛性是super-linear的，具体的收敛阶是黄金分割数。

重根的情况

会退化成FPI：

9.png

如果是已知重根个数，可以这样来改进：

8.png

具体来说就是当成FPI来处理，然后让迭代式在根处一阶导为0，这样的FPI就是二阶收敛了。

image-20220517113424420.png

提示一下这里的的处理，可以参考的那个展开，然后代换一下就欧克了。

如果布吉岛重根个数，可以这样考虑，把求的重根问题转换成求零一函数的单根问题，然后就能用标准Newton迭代法了捏。

image-20220517114403968

设是方程根的阶迭代函数，那么是方程的阶迭代函数。

这个证明用到了一个构造，就是如果是阶迭代函数，就可以写成这样的形式，其中。

然后就是朴实无华的泰勒展开即可。

迭代序列的收敛问题，数列收敛

收敛阶数

泰勒展开

线性方程组解法

表示第次消元后得到的结果，可以参考课本。

Direct method for solving systems of linear equations这部分真没啥好说的，看ppt吧，比较显而易见的东西了已经是。

这里总结一下各种方法的计算技巧：

  • Doolittle算法是中的的对角为单位，按照行列的顺序去求解。
  • Crout算法是中的的对角为单位，按照列行的顺序去求解。
  • Cholesky算法是按照列对角元素的顺序求解，计算一列再算下一个对角元素就行了，不需要计算行的。
  • 改进的Cholesky算法是按照先求再去按列算的顺序，求的过程其实就类似于Cholesky算对角元素，然后再去算列。
  • 三对角追赶法，其实就拿Crout分解就行了，记住基本就完事了，然后按照行对角元素的顺序求解，那个给的公式可记可不记。

矩阵的条件数和误差分析

稍微讲一下迭代法吧：

矩阵迭代消元可以看成一种FPI，但是有些不同的是对于equation不能孤立地去看，，因为方程组之间是联系的，所以当成一个整体用矩阵的性质来判断收敛性，或者可以说把 vector当成一个整体来看，去研究收敛性。

Jacobi Method

这定义已经简单明了了，相当于是把具体的操作用矩阵的形式进行了描述。

image-20220521225628176

这边给个例子：

image-20220521230022035

收敛性：

严格对角占优，谱分析里面经常出现的条件了属于是

image-20220521225713623

Gauss-Seidel

其实就是用更新过的值去迭代

image-20220521230117546

这边也给个例子吧

image-20220521225957854

Successive Over-Relaxation (SOR)

image-20220521231338424 image-20220521231355446

收敛性

image-20220521231905778

证明细节在这，感兴趣自己看看：https://math.stackexchange.com/a/126496/980786

image-20220526224512482

这部分证明很多，建议是直接背ppt的结论就可以了。

Jacobi和Gauss-Seidel收敛性的充分条件

image-20220521232252719

SOR收敛性的充分条件

值得一提的是Gauss-Seidel本身也算是的情况。

image-20220526222135212

Jacobi收敛性的充分必要条件

image-20220526224334036

或者按照迭代式收敛那个来，也就是看

这个误差估计参考FPI的即可。

image-20220526222556827

好题

26，31

程序设计

Gaussian 列主元消元法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
function x = Guass_Elimination(A, b)
format long;
n = size(A, 1);

for i = 1 : n - 1
    % find pivot
    [~, p] = max(abs(A(i:n,i)));
    p = p + i - 1;
    if A(p,i) == 0
        fprintf("Not Singular!");
        return;
    end
    temp = A(p, 1:n);
    A(p, 1:n) = A(i, 1:n);
    A(i, 1:n) = temp;

    
    temp = b(p);
    b(p) = b(i);
    b(i) = temp;
    
    % Elimination
    for j = i + 1 : n
        m = A(j, i) / A(i, i);
        A(j, 1:n) = A(j, :) - m * A(i, :);
        b(j) = b(j) - m * b(i);
    end 
end


x = b;
for i = n:-1:1
    for j = i+1:n
        x(i) = x(i) - A(i,j)*x(j);
    end
    x(i) = x(i) / A(i,i);
end

插值

拉格朗日插值法

数学原理

首先是插值的概念：对于点，函数满足，则称是这些点上的插值函数。

其次为什么我们选用了多项式插值，这是因为

  1. 多项式具有良好的数学性质，首先多项式插值有Main Theorem，也就是存在唯一性定理，保证了计算的唯一和有效性，而且有很多涉及多项式的数学理论可以使用，例如泰勒展开，方便收敛性证明和误差估计。
  2. 其次多项式的计算对于计算机硬件来说是更加快速有效的，在实际应用中效果很好。

对于数学性质，这里简单介绍一下唯一性：

Let be n points in the plane with distinct . Then there exists one and only one polynomial of degree $ n − 1$ or less that satisfies $ P (x_i) = y_i$ for $ i = 1,…,n$

接下来介绍拉格朗日插值法，既然已经有了存在唯一性定理，那么只要设计——出一种算法能获得不超过次的多项式，最后的结果都是唯一的。

拉格朗日插值法就是利用了一项对应一个插值的坐标点，

我们希望带入第个点时，只有，其余，根据零点来构造多项式，利用带入得到1的性质，得到对应的系数，因此不难得到表达式：

这就是拉格朗日插值法的数学原理。

考虑截断误差

image-20220521095942613 image-20220521100015986

误差估计可由此式推出：(个点的情况)

但是通常来说不能确定，而是给出一个的上界，作为误差估计的上界，另外当为任一个次数小于等于的多项式时，根据误差表达式可知此插值多项式是精确成立的。

代码

Lagrange interpolation

Input: vector and , the test vector

Output: prediction 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
function [y_predict] = LagrangeInterpolation(x_data,y_data,x_test)
% n+1 data points, find a n degree poLynomiaL interpoLation
n = length(x_data) - 1;

% m is the length of the test data
m = length(x_test);
% k is the counter
k = 1;
y_predict = 0;
% index from 1 to n
while k <= n+1 
    L = ones(1,m);
    for j = 1 : n + 1
        if(k ~= j)
            L = L .* (x_test-x_data(j))/(x_data(k) - x_data(j));
        end
    end
     y_predict = y_predict + L*y_data(k);
     k = k + 1;
end

% Output
fprintf("The answer is:\n");
for i = 1 : m
    fprintf("(%f, %f) ",x_test(i),y_predict(i));
fprintf("\n");
end
end

Newton插值法

Lagrange方法在需要增加节点时需要重新计算表达式，十分不方便，而Newton插值的思路就是希望每增加一个节点时，只附上一项上去即可。将改写为

这个求解的过程需要用到差商的概念，因为差商是涉及这种连乘的多项式形式和对应点的函数值。可以先带一个和进去，发现对应应该是，应该是，剩下可以用数学归纳法得出其实就是。

差商

接下来介绍一下差商相关的知识：

  • 阶差商必须由个节点构成，规定为零阶差商。

  • 差商的构造方法： ，比如说要构造阶差商，只要在这个点中随便挑两组不同的点组成阶差商，然后相减，对应分母取缺的项之差即可。

  • 差商是具有对称性的，差商的值是和的顺序无关的。

  • 阶差商和阶导数有一个关系式，等距情况下阶差商和阶差分就是差个系数的关系。

image-20220521194617046

等距Newton插值法

前插的话是这样的：

后插的话是这样的：

image-20220521224127209

然后把，这里前插的话，后插的话，然后和对应前插后插式子带入即可。

得到前插公式：

后插公式：

其实这里就是

差分和函数值的关系：

这里引入了一个平衡算子和差分算子，定义是。
那么很显然

函数逼近

建议看https://zhuanlan.zhihu.com/p/138011852

这里我先暂时不写了哈

积分

这章讨论的都是基于插值的数值积分方法，由插值那章得到的理论可以直接套过来，比如代数精度，在数值积分上也有体现。

image-20220523225156795

Trapezoid method

Simpson method

余项就是Language插值余项积分的结果

Newton-Cotes

为偶数对应的Newton-Cotes方法是阶的原因是，最后一项阶导数对应的那个项积分出来应该是0，因为区间对称而且是奇函数。

加上了等距的条件后，上面的式子都可以对应进行简化，将完全与区间无关的部分计算出来，就是Cotes系数了。

composite Trapezoid method

image-20220527211248767

composite Simpson method (integer)

image-20220527211309761

实际中去用的话可以这样去写：个interval里面分别用composite rule，

数值稳定性

当Cotes系数全正时，该方法是稳定的。

龙贝格积分

数学原理：

Romberg Integration可以视为composite Trapezoid Rule和extrapolation的结合。

所以首先从这两个方法谈起，受插值函数的启发，提出了Newton–Cotes formulas用于计算积分，也就是利用原来的等距插值多项式去积分，degree为1的情况就是Trapezoid Rule，degree为3的情况就是Simpson‘s Rule。但由插值那节可以得知，插值多项式并不是次数越高越好，所以对于一个较大区间的积分问题，可以分割为小区间的Trapezoid Rule或者Simpson‘s Rule，这也是就composite Trapezoid Rule和composite Simpson’s Rule的思路。

对于这样得到的公式，还可以在误差上继续提升，这里就要用到extrapolation了，具体来说是Richardson’s Extrapolation，我们将误差视为高阶多项式，进行展开，然后利用步长更小的表达式迭代将误差缩小。

以下是具体定义和公式：

Definition: The degree of precision of a numerical integration method is the greatest integer k for which all degree k or less polynomials are integrated exactly by the method.

composite Trapezoid Rule:

We can write it as:

ps: 这里写成这样书上只说了 By an alternative method, it can be shown that if , the Composite Trapezoidal rule can also be written with an error term in the form.

具体的证明见以下资料：https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.89.7042&rep=rep1&type=pdf

Let

这里说一下的含义，第次二分，那么原来的interval就被分为个区间，而新增的节点数量，应该是个，这些节点的分布也是按照了odd的次序，因此是。

Then we can get

当计算得到的的时候，就是符合了预设的精度。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
function R = Romberg(f, a, b, n, epsilon)

h = b-a;
R = zeros(n,n);
R(1,1) = h/2 * double(f(a) + f(b));

for i = 2:n
    R(i,1) = 1/2 * (R(i-1,1) + h*sum(f(a + ((1:2^(i-2))-0.5)*h)));
    for j = 2:i
        R(i,j) = R(i,j-1) + (R(i,j-1)-R(i-1,j-1)) / (4^(j-1)-1);
    end
    
    if abs(R(i,i) - R(i-1,i-1)) < epsilon   
        break;
    end
    
    h = h/2;
end

% remove the redundant 0 in the matrix
R(:, all(R == 0, 1)) = [];
R(all(R == 0, 2), :) = [];
R = vpa(R,16);



微分方程

Latest update: 2022/5/2

对于常微分方程问题，课本所提及的主要是一阶的，也就是和的关系。

Background: 解析解只能适用部分问题，大部分实际问题还没解决，数值计算的方法正可以解决这样的情景。

Motivation: 现在目前所有的只是初值，也就是的表达式，还有的区间。微分方程的解其实就是满足这样equation的函数，所以我们现在的目标可以定为逼近这样的函数，朴素的idea：由一点出发，通过导数移动小距离，一点一点逼近，将误差控制到足够小。因为我们考虑最后要求和足够近似，这样的话可以考虑导函数的插值积分，不同阶的插值其实就是对应Adams多步法。如果只是考虑一个点的话，那可以考虑用泰勒展开来逼近这点的局部。

单步法

Euler’s Method就是基于这种思想最朴素的方法，利用了1阶的泰勒展开，或者说导函数一个点的插值，迭代式如下

但是这个初值问题解的Existence, uniqueness, and continuity for solutions还没确定，于是利用以下理论确定(具体证明省略)：

Start

A function is Lipschitz continuous in the variable on the rectangle if there exists a constant (called the Lipschitz constant) satisfying

for each $(t , y_1), (t , y_2) $in .

A function that is Lipschitz continuous in y is continuous in y, but not necessarily differentiable.

We can also change the condition a little bit:

Suppose is defined on a convex set . If a constant exists with

then satisfies a Lipschitz condition on in the variable with Lipschitz constant .

Assume that is Lipschitz continuous in the variable on the set and that . Then there exists between and $b $ such that the initial value problem

has exactly one solution . Moreover, if is Lipschitz on , then there exists exactly one solution on .

End

然后也可以顺便推出Euler’s Method的误差

其中的和是两个不同的初值条件。

对于实际序列来说

详见here

但是这里有个问题在于有时必须要取很小才能得到比较好的结果，那能不能在这个误差的基础上优化，也就是误差上界是甚至更高的多项式，这样收敛就更快了。

由local truncation(one step error) 启发，提出了Taylor method，也就是原来的再多展开多阶：

where

具体来说是二元函数的泰勒展开：(注意这里的可以李姐为上面的)

泰勒展开和全微分差别留意一下

这样确实增加了准确度，但是求导对于数值求解是复杂的，现在将导数换为由已知的和的组合来去approximate，也就是展开$ a_1f(t + \alpha_1, y + \beta_1)$，求解能大大简化，针对于二阶展开的情况，

match coefficients:(get mid-point method)

More generally, we get this form

set 就是Explicit Trapezoid Method

set 就是Midpoint Method

而四阶龙格库塔其实就是三阶展开的情况：

单步法的收敛性

Definition:

A one-step difference-equation with local truncation error is said to be consistent if

A one-step difference equation is said to be convergent if

where is the exact solution and the approximation.

image-20220518234345523

We can just take the mid-point method for example:

If is Lipschitz with constant ,

Then we can get is also Lipschitz.

Local truncation error theorem

image-20220519095834966

Taylor Method收敛性

对于Taylor Method的误差是这样的：

image-20220519095000831 image-20220519095032583

RK method收敛性

对于RK method的误差是这样的：

image-20220519105958689

这个就太复杂了，这里其实只要记住作为Taylor method的变体就行，局部截断误差的阶其实都差不多

image-20220519110243281

然后对于实际也不可能真这么算局部截断误差，可以考虑说利用已知的值和近似来估计截断误差的值，下面是解释，比较简单直白了。

image-20220519111520186

多步法

多步法的优势：Multistep methods can achieve the same order with less computational effort—usually just one function evaluation per step.

Reason: After the fifirst few steps, only one new evaluation of the right-hand side function need to be made. For one-step methods, it is typical for several function evaluations to be needed. Fourth-order Runge–Kutta, for example, needs four evaluations per step, while the fourth-order Adams–Bashforth Method needs only one after the start-up phase.

线性多步法

线性多步法的intuition很简单，就是利用泰勒展开的逼近，可以得到足够阶数的截断局部误差。

公式推导的过程十分朴实无华，左右两边泰勒展开即可

可以得到。

这里面的为1 or 0 对应的是隐式和显式。

对于控制参数即可。

Adams方法

intuition在开头就说了，这里是用插值得到积分作为去逼近。根据前个数据点构造的向后次插值多项式

其中

用代替在上数值积分，令，此时

这块后插不熟的建议remake一下捏。

提示一下：

后插的话是这样的：

然后把和上式带入即可。

线性多步法的收敛性

root condition

image-20220519115508875 image-20220519115544190

然后对于这个consistent，可以用两个特征多项式的关系，代表的特征多项式，代表的特征多项式，然后

是线性多步法相容的充分必要条件。

代码

四阶龙格库塔

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
function [y_ans] = Runge_Kutta(a, b,y_0 ,n ,f )
h = (b-a)/n;
x_0 = a;

y_ans = ones(1, n);
y_ans(1, 1) = y_0;
fprintf("(%f, %f)\n",x_0, y_0);

for i = 1:n
    k_1 = h * double(f(x_0, y_0));
    k_2 = h * double(f(x_0 + h/2, y_0 + k_1 / 2));
    k_3 = h * double(f(x_0 + h/2, y_0 + k_2 / 2));
    k_4 = h * double(f(x_0 + h, y_0 + k_3));
    
    x_0 = x_0 + h;
    y_0 = y_0 + 1/6 * (k_1 + 2 * k_2 + 2 * k_3 + k_4);
    y_ans(1, i+1) = y_0;
    fprintf("(%f, %f)\n",x_0, y_0);
end