概率和测度(ZJU大佬)

本系列为搬运,原作者是ZJU的巨佬,写的很好,但是这几篇博文代码挺不规范的,zxr就顺便魔改了一下

概率与测度 (1)：关于测度 « Free Mind (pluskid.org)

概率与测度 (2)：积分与期望 « Free Mind (pluskid.org)

https://blog.pluskid.org/?p=799

概率与测度 (4)：闲扯大数定理与学习理论 « Free Mind (pluskid.org)

顺便提示一下，看这个系列前最好把这个系列看完

【测度论】Ch1. 问题引入 - 知乎 (zhihu.com)

补充：重新审读搬运的内容发现和原网站不符，渣浪的版本很多错误，无语(ˉ▽ˉ；)…，又花了很大功夫进行了魔改

“Probability theory is measure theory with a soul“ — M. Kac
概率论是有灵魂的测度论

概率与测度 (1)：关于测度

我又来挖坑了。因为打算抽时间（比如下学期或者下下学期）来学一下概率论，所以学习过程中的一些感想或者笔记什么的应该会不定期地整理出来。这算一个开头吧。

其实概率论似乎经常处于一个比较尴尬的地位，在历史上一度被认为并不属于数学的一部分，直到将测度论引入以建立起严格的公理体系之后，才被数学界所承认。当然，说它“不是数学”，仅仅就是字面上的意思，并没有说什么东西不是数学就一定是不好的。事实上，在被严格化之前，概率统计作为一种工具就已经被广泛应用到各个领域中了，当然，在严格的理论体系建立之后，不论从理论上还是应用上，都得到了爆炸性的发展。然而，仅从大学的教育来看，概率论似乎仍然处境尴尬。

比如在 ZJU 本科，似乎概率论是像 C 语言一样的全校必修的一门课（我从来没有搞清楚过学校的选课规则，以前选课大致都是跟风室友的），足见其用途之广泛。然而除了理学院的一些专业之外，其他专业的概率论教学并没有得到近代概率论的严格化所带来的好处。或者说，这样的东西在这样的上下文下原本就是不需要的吧，毕竟对于工科甚至文科的学生来说，概率就是一种工具而已。其实大部分时候都没有什么问题，但是一些模糊的没有良好定义的概念，有时候会带来问题，看看网络上各种流行的概率相关的趣味问题，比如好像有一个问题是说，有三扇门，其中一个后面有奖励，让你任选一扇门，然后主持人打开剩下的两扇中的其中一扇给你看后面没有奖励，然后问你要不要放弃最开始的选择，而选剩下的那一扇门。类似的问题经常会引发大量的争论，大家各执一词，互不相让，许多情况下引起争议的根源都来自于其中有一些“看起来很明显”但是其实并没有经过严格定义的术语的理解的偏差。

另一方面，虽然数学系的概率论课程确实从严格的角度来教授了，但是听我身边认识的数学系的人说来，他们专业的好多人其实都并不对概率论这门课很有兴趣。因为大家选了两门课“概率论”和“实变函数”，然后发现两门课讲的东西差不多是一样的。实分析课上讲测度论，而概率差不多就是一个归一化了的测度，于是大家都有一种“被坑了”的感觉。 ^_^bb

当然，我在工科学到的概率论也就是一些技术性的东西，甚至感觉就是中学学过的一些东西的再总结，以至于当时感觉好像没学什么一样，而从最开始接触概率就一直让我很困惑的一些细节上的问题也一直未能解决。比如学完之后仍然不知道所谓的“概率”到底是什么东西，好像说是“频率”的极限情况，但是当人们谈论“彗星撞到地球的概率”时，难道是指“彗星一共经过了多少次，其中有多少次撞到地球上了”这一频率的极限吗？那地球真的要万劫不复了。

再比如最让我不爽的是，在离散的情况下，比如，扔骰子，我们会讨论骰子的正面数字等于几的概率，例如通常情况下我们都认为。然而到了连续情况下就又换了一套体系，搞出了一个什么概率密度函数，虽然积分一下能够得到一个和离散情况下有点像的概率分布函数，但是仍然是考虑的，但是却不能谈论“等于某个值”的概率了，或者说，根据积分来看，这个玩意它等于零。这件事情让我在和离散情况下进行类比的时候产生了困难，因为从一开始就是一一种“直观”的方式来引入这些概念的，现在突然又不直观了，就让人感到很沮丧。而且，我一直对于这件事情耿耿于怀，虽然我知道通过怎么样的计算能够得到它确实等于零，但是这并不是一个很让人满意的理由。就好比你问食堂师傅为什么大排涨价了，他告诉你因为市场上的大排都涨价了，所以我们食堂也涨了——虽然是回答了你的问题，但是你依然会很郁闷。但是如果师傅告诉你因为天蓬元帅带着猪们起义了，地球上大批猪军团逃亡到月亮上了，所以猪肉短缺，导致大排涨价了，你就会觉得，哦，原来如此！天蓬元帅真是太帅了！这种感觉，就是当我得知“概率就是测度”时候所感受到的——之所以等于零，是因为这个时候单点集的（Lebesgue）测度为零。如果一开始就以抽象的方式来引入，到最后说得再抽象也总是可以接受的咯，不过，这种描述方式最美妙的地方在于，离散和连续的情况是可以统一描述的——这一点才是让我纠结的结症所在呀。

于是言归正传，还是从测度论开始说起吧。测度 (measure) 可以看作是测量一个集合的大小而引入的一个概念。当然，关于集合的大小，我们本身已经有了一个概念叫做集合的 Cardinality ，也就是数集合元素的个数。在有限集上，这是很有用的，然而在无限集的情况下，这种“测度”（暂且这样称呼它，虽然我还没有明确定义什么是测度）就显得过于粗糙了。例如，在实数轴上的一个区间，它的元素个数是（不可数）无穷多个，并且任意两个区间的 cardinal number 都是相等的，这（对于我们目前要做的这件事来说）并不是很有用。然而，另一方面，对于这些连续的集合，我们又有自然的“体积”的概念，这里的“体积”是一个宽泛的概念，比如，在一维空间下，就是“长度”，二维空间下是“面积”，三维则是我们传统的“体积”。因此在无限集的情况下我们通常需要另外的测度，最好是和我们熟知的“体积”的概念相容。所以，测度这个抽象概念的引入，可以说是为了得到一个统一的描述框架吧。

一方面，我们希望通过定义一个测度来测量集合的大小，它需要能够处理各种情况，包括有限集、无限集甚至是各种抽象的集合；另一方面，我们希望在某些特定的情况下，它要和我们熟知的一些东西相容：比如一个区间的长度（测度）等于区间端点之差的绝对值，以及两个没有相互重叠的正方形构成的图形的面积（测度）等于它们各自的面积（测度）之和，等等。到了这里，设计一个测度就好像变成了制造一把尺子（或者量筒什么的，如果考虑多维的情况的话）。既然是尺子就有它的测量范围——也就是哪些对象是可以用这个尺子测量的，例如用一个普通米尺来测量地球的半径估计会很有困难，或者用它去测量原子的半径也是 mission impossible 。实际上，在从小大到的教育中我们就被灌输了一个测量仪器的可测量的范围是测量仪器的“有机组成部分”，非常重要，依稀记得高中物理中诸如千分尺和游标卡尺的精确度和测量范围等等都是考试中经常会出现的内容。在测度论里这个问题同样重要：在定义一个测度的时候，我们需要同时定义哪些集合是“可测的” (measurable) ——也就是可以用这个测度来衡量的。我们通常在一个空间 Ω （可以看成一个“全集”）里来考虑问题，需要测量的元素就是 Ω 的子集，其中所有可测的子集构成的集合，记为，这个就是测度的定义域。实际上我们还要求构成一个-Algebra（概率里通常称为 -field ），不过我们暂且先不管这个。然后，我们将一个测度定义为一个函数（注意：可以取到正无穷)，并且满足如下两条：

对于空集有，
满足可列可加性，也就是说，如果，其中和都是 -可测集，并且互不相交，那么我们有。注意有限可加的情况包含在这里了。

任何这样的一个函数都叫做一个测度，当然，我们知道和是息息相关的，通常我们把放在一起，叫做一个测度空间 (measure space) （注意不要和“度量空间” metric space 混淆了，后者测量的是两点间的距离，这里我们关心的是集合的大小）。

现在让我们先把抽象的定义放一放，看看实数轴上的情况，也就是说，。一个最简单的例子就是令为所有区间组成的集合，而定义，其中为区间的长度，也就是两端点之差。容易验证，这符合测度的定义。这个定义虽然和我们所熟知的区间长度相吻合，但是，这把尺子可以说是功能相当有限，因为它只能测量区间，例如这个集合，就没有办法用这把尺子来测量，因为它不是一个区间。这多少让人有点失望，因为我们目测一下这个集合的大小“明显应该是” 2 嘛！——或者说，根据我们的 intuition ，我们希望它的大小应该是 2 的。这样一个连我们眼睛目测都比它好的度量，果断应该扔掉了！实际上，对于实数集这么具体的一个集合，我们当然要有点野心：希望定义一个测度，使得的任何子集都是可测的！

这件事情其实很容易，例如我直接定义一个测度让它恒等于零就可以了，这样实数的任何子集都是测度为零的可测集。不过这显然不是我们想要的，用抽象的东西来建模我们熟知的概念的时候，通常都希望能够保持住一些我们所熟悉的法则。比如，在实数轴上，我们希望定义的测度用来测量一个区间的时候，是和区间本身的长度是相等的。除此之外，我们还希望测度具有平移不变性，也就是说，如果是可测集，那么也可测并且等于，其中是一个实数，$x_0+A= { x_0+x |x \in A } $ ，也就是将集合沿数轴平移所得到的集合。这也是很符合我们直观的一点要求，实际上我们在很多地方都“偷偷地”有假定某些性质具有平移不变性，比如关于三角形全等的问题，如果一个三角形在空间中移动到另一个地方之后（面积、周长或者边长之类的）不能保持不变的话，全等的问题就很难说了。

不过，悲剧的是，明明看上去都是很合理的要求嘛，加到一起，“神”就不认账了，怎么都不让我们造出这么一把“尺子”来——不是工艺水平不够，而是根本就造不出来。下面我们就来证明，对于任意满足上面条件的测度，总可以构造一个的子集，使得它是 -不可测的。这个构造可以在几乎任何实分析的书上找到，但是具体还是比较 technical 的，如果不感兴趣可以先跳过。

在本节的后面

这样一来，我们的美梦就破灭了，因此不得不做一些折衷。允许不可测集的存在，这样一来，我们的测度的定义域就不能是所有子集了。例如，在实数轴上，在分析中很常用的一个测度是 Lebesgue 测度，它具有上面说的几条性质，因此以上面的方法构造出来的不可测集也是 Lebesgue 不可测的。Lebesgue 的测度可以通过一个叫做外测度的东西引入。在实数轴上这样来定义一个集合 A 的外测度

这里是一列有界的区间，也就是说外测度是所有覆盖 A 的区间长度和的下确界。注意这个值总是存在的（有可能等于正无穷），因此对于的任何子集，外测度总是有定义的。不过外测度并不满足可列可加性，而是满足一个叫做次可加性的性质：

只能取到不等号。因此，虽然其他几条（非负、平移不变、单调等）都满足，但是外测度并不是一个测度。但是外测度是可以度量的所有子集的，所以说也是有得必有失呀。另外这里还要注意一点用词，数学里似乎经常会出现这样的“白马非马”的名词，比如“外测度 (Outer measure)”并不是一个“测度 (measure)”，还有诸如“带边流形 (manifold with boundary)”并不一定是一个“流形 (manifold)”等等，看起来好像都是随手取出来的名字，但是由于历史原因也一直沿用了，而且似乎一时也想不出什么更好的名字来。 anyway ，这个不是重点。

根据次可加性，我们可以得到，对于任意集合和，有

如果这里是个测度的话，不等号里的等号就应该成立了，但是刚才我们也看到了我们没有办法在所有的子集上定义测度，于是我们直接将“Lebesgue 可测集”定义为使得上面的式子中等号成立的那些集合。更具体地来说，一个集合 E 被称为 Lebesgue 可测的，当且仅当对于任意集合 $A\subset \mathbb{R} $，满足：

注意由外测度本身的性质已经得到了反方向的不等号，再根据这个方向的不等号，实际上就可以得到等号成立：

将外测度限制在所有的 Lebesgue 可测集上，我们就得到了 Lebesgue 测度。也就是说，如果 E 是一个 Lebesgue 可测集，那么我们的 Lebesgue 测度在 E 上的取值就是它的外测度。可以证明，这样定义的 Lebesgue 可测集构成一个 -Algebra （就是说，如果可测，那么也可测，等等），并且，这样构造的 Lebesgue 测度满足可列可加性。

这个测度在分析里用得很多，因为它可以用来定义 Lebesgue 积分——可以看成 Riemann 积分的一种推广，具有更多优良的性质。当然这里的积分的也是概率论里的重要基础概念，不过在讲积分之前，先看几个 Lebesgue 测度相关的性质。以下如非特别说明，都用“可测”代替“ Lebesgue 可测”，因为写起来真是好长…… =.=

首先，任意外测度为零的集合都是可测的。这个很好证明，假设，那么对任意集合，我们有，由外测度的单调性，有，再由外测度的非负性知。另一方面，又有，再利用外测度的单调性，即可得到

即证明了是可测的。关于零测集，也是比较有意思的，根据外测度的定义，我们可以证明，实数轴的任意有限子集是零测集，不仅如此，任意可数子集也是零测的，比如，所有有理数组成的集合的 Lebesgue 测度为零。这在直观上也是可以理解的： Lebesgue 测度主要是用来测量“区间长度”这个尺度下的度量，任意一个区间都包含了不可数无穷多个点，因此像有理数这种只有可数无穷多个点的集合，也就只有沦落到测度为零了。不过，也并不是包含了不可数个点，就能保证测度非零的，最著名的例子当属 Cantor set 了：这个奇葩的集合包含了不可数无穷多个点，但是它的 Lebesgue 测度为零。

本来打算接下去介绍通过 Lebesgue 测度来定义的 Lebesgue 积分的概念，从而很自然地得出概率论中的几个基本概念，并解决那个困扰我许多年的“问题”。然而发现这个篇幅好像已经太长了，于是索性留到下一篇再接着吧。

构造不可测集

本来暂时还不想解释 -Algebra ，但是发现下面在构造的时候频繁要用到这个结构，于是在构造之前先简单介绍一下这个东西。一个 -Algebra 可以定义为一个全空间的子集构成的集合，使其满足，并且其中的元素在集合的补运算和可数并运算下封闭。换句话说，如果 $ A\in\mathcal{A} $，那么必须要有补集 $ A^c=\Omega-A\in\mathcal{A}$ ；如果 $ {A}{i=1}^\infty$ 是可数个中的元素，那么它们的并也属于其中： $\bigcup{i=1}^\infty A_i \in\mathcal{A} $。

根据这个条件，我们可以证明测度的单调性，假设都是可测集，那么由测度的非负性，立即得到

注意这里即使我们有真包含关系，也并不一定能得到严格的不等号，这是由于有零测集的存在，后面再说。接下来我们开始构造这个奇葩的不可测集。首先从区间 [0,1] 开始，根据前面的要求，我们有。现在我们在这个区间内定义一个等价关系当且仅当 $a-b\in \mathbb{Q} \mathbb{Q}$ 表示有理数。这个等价关系将划分成一些互不相交的等价类，现在我们从每一个等价类里选取一个元素，构成一个集合 C （根据选择公理，这样的集合是可以构造出来的）。下面我们用反证法证明 C 就是一个不可测集。

令为 -1 到 1 之间的所有有理数，显然 $\mathbb{Q}’ $是可数的。对于每一个 $q\in\mathbb{Q}’ q+C$ 构成的一个平移，假设是可测的，那么也是可测的，并且。根据 -Algebra 的定义，也是可测的。此外，我们还有对于任意不相等的$ q_1,q_2\in\mathbb{Q}’$ ，。这个很好证明，假设不是这样，那么我们有 $x_0\in (q_1+C)\cap(q_2+C) $，于是，其中。于是根据前面等价类的定义，和应该是属于同一个等价类，但是我们在构造集合 C 的时候只从每个等价类里选择了唯一的一个元素，因此必须是，又由于，知道，矛盾。故和$ q_2+C$ 互不相交。

由于任意平移两两互不相交，由测度的可列可加性，我们有：

由于我们假定 $C \mu©$ 应该是一个确定的数，如果，后面这个级数也等于 0 ；如果，那么这个无穷项求和将得到。为了方便，我们将这个值记为$ L$ 。下面我们证明既不能等于 0 也不能等于，从而得到矛盾，因此不可能是可测的。

首先注意到，对于任何，它一定属于我们之前得到的那一堆互不相交的等价类中的一类，也就是说，存在一个，使得$ x^-c^=q^*\in \mathbb{Q} $。又由于和都是区间中的数，所以它们之差被限制在区间内，因此。也就是说，实际上属于我们上面构造的众多互不相交中的平移中的某一个。由于是任取的，我们得到如下包含关系：

由测度的单调性，我们有，因此不能等于 0 。另一方面，由于里的每个数都是在区间内的，而 $C $里的数则在内，因此所有的平移，以及它们的并组成的集合中，所有的数字都不会超出区间。再一次利用测度的单调性，我们得到，从而 L 也不可能等于。于是我们证明了 $C $是不可测的。

概率与测度 (2)：积分与期望

上一次我们谈到零测集的概念。之所以提出来，一方面是因为它比较好玩，另一方面是它和另一个重要概念息息相关。这个东西就是“几乎处处 (Almost everywhere)”，经常被缩写为“a.e.”。例如，“函数几乎处处等于零”――当我第一次看到这个样子的话的时候，就被深深地雷到了。 =.=bb 当然，我是后来才知道，这个东西是有严格定义的。把一个听起来就模棱两可的词强行加上一个严格的定义，然后直接拿来用，果然搞数学的人好洒脱！

回到 a.e. ，它的定义其实很简单，我们说某个性质“几乎处处”成立，严格地来说，就是在讲它除了在一个零测集上不成立之外，在其他地方都成立。例如，传说中的Dirichlet function，它在有理数上取值为 1 ，在无理数上取值为 0 （题外话：这个玩意它还是一个处处不连续的函数）。注意到的 (Lebesgue) 测度为零的，因此除了在一个零测集上之外，其他地方都取值为零，那么我们就说它“几乎处处为零”。

和这个对应的概率论里常用的还有一个看起来更雷人的概念，叫做 almost surely (或者叫做 almost certain 、almost always) ，说某件事情 almost surely 成立，就是说这件事情在一个“满测度”集合上成立。所谓“满测度”集就是说它的补集的测度为零，而并不一定要求补集是空集。不过零测集和空集之间的关系，如果不严加定义的话，仅用文字描述起来很难搅清楚，而用上了 almost surely 这样的看起来很模糊的词，就更加雪上加霜了。也许，都是那些数学工作者的错——选了一些表面上看起来很混淆的用词，结果导致一些人在并不知道真正严格含义的情况下纠缠在字面上的意思，最终沦落为民科啊……

当然，抛开用词不说，a.e. 的引入在实分析中是必要的――而并不只是简单的把原来的一些“处处成立”的定理推广为“几乎处处成立”这样一个看上去无关痛痒的扩展。可以想像一下，应该是某个定理在条件中不是 a.e. ，但是结论只能得到 a.e. ，所以说如果去掉 a.e. 这个概念的话，整条路就走不通了。不过，这里暂时还没法详细说这个问题。于是下面以一幅 6 格漫画结束开场白，正式进入这次的主题――“积分”吧！

2011.05.23-天气预报.jpg

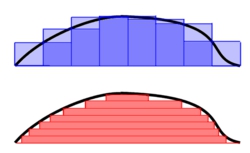
微积分现在几乎是所有专业的大一必修课了吧，在微积分课程里讲积分的时候，我们都还记得，积分就是用一堆长方形条来近似一个函数图像“下”面的面积――如右图中蓝色的那个图。这样的积分叫做黎曼积分 (Riemann Integral)，而这次要讲的积分叫做勒贝格积分 (Lebesgue Integral) ，一般最常用的示意图是右边红色的那个。从对比图中可以看到，黎曼积分是对定义域进行划分，而勒贝格积分是对值域进行划分。表面上看起来似乎是一个比较无聊的变化，但是实际上这个简单的变化使得勒贝格积分的应用范围相对于黎曼积分来说大大推广了。

当然，对于我们普通的实函数来说，似乎直观上看不出太大的区别（稍后我们会说，即使这种情况下也是有很大区别的），但是考虑推广的概念：称为一个映射，如果对于每一个，由给定一个。这里和分别称为映射的定义域和值域，当值域是或者其子集时，我们通常将映射称为“函数”。也就是说，我们可以在一个抽象的空间中定义函数，但是如果要对这样的函数进行积分的话，黎曼积分就派不上用场了，因为你没有办法直接在一个抽象的空间里做“划分”，但是勒贝格积分却可以做，因为对于一个“函数”来说，值域总是实数，在实数集上做划分是我们已经熟知的工作。

当然，除了这一个直观上显而易见的好处之外，勒贝格积分相对于黎曼积分还有一大堆优点――当然，黎曼积分也有它自己的优点，最明显的一个大概就是它是方便计算的吧，大部分函数直接按照勒贝格积分的定义来进行计算会是相当繁琐的一件事情（幸运的是当一个函数是黎曼可积的时候，它的黎曼积分和勒贝格积分是相等的），我想这也许是微积分里要讲黎曼积分而不是直接讲勒贝格积分的原因吧，在实际中会更有用一点，而且也不需要测度方面的准备知识就能讲。

不过，如果我们想要在抽象的集合上定义概率的若干基本概念，就必须要用勒贝格积分。前面的直观解释虽然看起来还蛮简单的，但是对值域进行划分也并不是简单地将“对定义域进行划分”的方法类比过来就行得通的，因为对于一个自变量，总是只有唯一的函数值，但是反过来，对于一个函数值，却有可能会有许多自变量与它对应。具体地操作起来，还需要借助于测度这个工具

都被画成我刚才展示的那张图那个样子（上面那张图来自于 wikipedia ），每次看到那张图我都会觉得非常 confusing 。左边这张图应该更为贴切一点：虽然按照值域进行了划分，但是最后得到的还是一个一个的“竖着的”（而不是像上面的图中那样“横着的”）矩形相加。比如，对于值域的某个区间，我们记（注意这只是一个记号，与是否有反函数没有关系）：

如果这个集合可测的话，那么我们用它的测度乘以“高度” ，就得到了一块面积。不过这块面积并不一定是一个矩形的面积，它可能对应许多个矩形，取决于集合的形状，如果它是一个单一的区间的话，那么就只对应一个矩形。不过现在的好处是，我们不用关心它的形状是什么，只要测度可以算出来就可以了。

白话解释已经足够多了，下面我们来把整个过S程说得稍微更精确一些。以下除非特别指明，都用“积分”来简称“勒贝格积分”。首先我们要引入“可测函数”的概念。称一个函数是可测的，如果它的定义域是一个可测集，并且对于任意的，集合 , , 等这些集合也都是可测的，这样一来，我们刚才的集合也是可测的――如果不可测的话，我们就没有办法算积分了。因此，我们的积分整个都是建立在可测函数的基础之上的――这并不是一个很大的限制，因为很多“有用”的函数都是可测的，包括一切（定义域为可测集的）连续函数等等。另外，可测函数的加和、乘积以及（几乎处处）逐点收敛的极限都还是可测的。

在可测函数中，有一类性质非常优良的函数，叫做简单函数 (Simple function) 。简单函数是一个取值为实数的可测函数，并且它的函数值只有有限个。例如，我们一开始提到的 Dirichlet function 就是一个简单函数，因为它的函数值只有 0 和 1 这两个值（并且显然还是可测的）。事实上，我们在那里用了个比较奇怪的记号，这个实际上是一类叫做indicator function的函数的通用记号（另外也常记作）。一个集合的 indicator function 是这样一个函数：

所以 Dirichlet function 实际上是有理数集的 indicator function 。用 indicator function 可以很容易来描述一个简单函数，假设简单函数的所有取值为，则我们有

简单函数乍看起来似乎不太简单，特别是像 Dirichlet function 这种处处不连续的函数居然也能混个简单函数的“户口”。不过对于定义勒贝格积分来说，简单函数确实是再简单不过了。首先我们从定义域的测度有限的情况开始考虑，如果是个如上形式的简单函数，它的定义域为并且

正是我们一开始白话中说的，将值域进行划分――由于这里的函数值只取有限个点，所以直接采用了最简单的单点划分，然后我们直接将每个函数值对应的定义域区间的测度相乘，再全部加起来就得到了。并且由于

到这里，勒贝格积分的最原始形式就已经初露锋芒了：Dirichlet function 这个东西由于太不连续了，黎曼积分是无法对它进行处理的。选择简单函数作为起点，一个是因为它简单，另一个是因为它性质非常好：对于任意一个定义在可测集（并没有要求测度有限）上的可测函数，存在上的一列简单函数逐点收敛于，并且满足。如果是非负函数的话，还能做到这一列简单函数是单增收敛于它的，这一点性质很好，利用这个，我们可以来定义非负可测函数的积分：

这里是一个非负的可测函数，而是一列单增收敛与的简单函数。可以证明，右边的极限总是存在的（如果把趋向于也看成极限存在的话），并且，还能证明右边的极限并不依赖于特定的函数列的选取。这样一来，非负可测函数的积分就定义好了。当这个积分小于的时候，我们称是（勒贝格）可积的。

最后，只要再推广到任意可测函数就大功告成啦！而这个推广也是非常简单的，对于任意可测函数，我们可以把它分解为正部和负部：，其中

都是非负可测函数，很自然地，我们希望将的积分就定义为

不过如果和同时为的话，这个式子就没有意义了。因此我们做一点限制，注意到也是一个非负可测函数，如果可积的话，可以得到和都是可积的（反之也对），这个时候上面的式子就不会出现无穷相减的问题。因此，对于任意可测函数，当非负可测函数是可积的时候，我们称是可积的，并用上面那个式子来定义它的积分。这样一来，我们的勒贝格积分终于定义好了！

勒贝格积分相对于黎曼积分有诸多好处，例如，可积当且仅当是可积的，但是黎曼积分得不到这个性质，还有通过控制收敛定理可以得到（收到控制的）可积函数的（几乎处处收敛的）极限也是可积的，并且极限的积分等于积分的极限。顺带一提，控制收敛定理的条件中只要求 a.e. ，这是一个重要的细节，如果不能保证只要在 a.e. 的时候就能成立的话，基于 Lebesgue 积分的后续一些理论就会出现困难了。如果以后有讲到这个内容再细说吧。

接下来让我们迫不及待地进入概率论的话题，当然其实也只是一个很小的序幕，把我们之前介绍过的测度和积分用一下，建立一些基础设施。不过这里其实也是非常简单的框架，在后续的介绍中说不定还会有一些变动。直接进入正题吧！首先是“概率空间”，其实就是一个特殊的测度空间：，其中就是一个集合，然后是可测集组成的集合（它是一个 -Algebra ），而是一个测度，这里我们额外要求，即全集的测度是有限并且归一化的。顺带一提，本文开头谈到的事件 almost surely 成立，到这里就有明确的意义了，其实就是。

在这种情况下，我们引入一些新的名词：归一化的测度被称作“概率”，里的那些可测集，被称作“事件”，而就是事件的概率了。下面举一个例子，考虑扔骰子，这个时候我们的对象集合包含了 1 到 6 这 6 个数码。接下来我们要在这个集合上定义一个测度。比如，我们尝试把它看成是实数集的一个子集，然后用我们之前说过的 Lebesgue 测度限制到这个集合上，可是我们知道勒贝格测度在有限集上的测度总是为零，对我们没有什么用，并且也没法满足归一化的条件。于是我们考虑另一种更适合这种情况的测度：counting measure，也许可以翻译做“计数测度”吧，顾名思义，它就是通过数对象的个数来计算测度的，在有限集上特别好用，它的定义为：

或者也有推广的定义，使得每个元素可以有一个权重：

接下来我们将它进行归一化，定义。注意我们的是个有限集，并且我们定义的这个测度在的所有子集上都可用的，所以可测集（也就是事件集合）就是所有子集。这样一来，我们的测度空间就构造好了，不妨设我们选取了不带权重的计数测度并进行了归一化，还记为。简单地计算就可以验证，这个玩意就和我们熟知的扔骰子的概率模型是一样的，比如：

不过这样似乎有点小题大做了，不过这个框架确实可以对问题统一地描述，下面再来看一个稍微抽象一点的例子，这个时候取集合为一个区间，并且直接用勒贝格测度和上所有的勒贝格可测集和的交构成事件集合（注意这个测度已经自动归一化了）。这样我们实际上就得到了一个――用我们熟悉的概率论的语言来说的话――在区间上的均匀分布。这个例子有点无聊，不过我想说的是，现在对于区间上的任意一个数，我们总是有（勒贝格测度在可数集上总是零），这就解释了我在上一篇中提到的那个从小就困惑我的问题：为什么在连续情况下我们不去谈论，或者说为什么它是等于零的。

接下来让我们再引入几个其他我们已经耳熟能详的名词――至少不能把费了这么大力气介绍的勒贝格积分给冷落了啊。在一个测度空间下的一个可测函数，我们把它叫做随机变量。事实上，我们可以把之前定义的“可测函数”的概念加以推广，到“可测映射”的情况，考虑两个测度空间和，以及他们之间的一个映射，如果对于中的可测集，我们总有在中可测，即，那么称是从到的一个可测映射。注意如果将空间取为实数集加上勒贝格测度，并取Borel 集作为可测集，那么此时的可测映射就和我们之前定义的可测函数是等价的――也就是随机变量了。

另外一些常见的情况，如果空间是，称为随机向量，是无穷维时称为随机序列，而当是一个函数空间时，则引出随机过程的概念。特别地，如果是一个简单函数――回忆一下定义，它的函数值只有有限个，那么我们得到所谓的离散型随机变量。

对于任意，由于是可测的，因此我们可以计算测度，通常情况下，我们还是将空间取作，而将勒贝格测度限制在该区间上得到归一化的测度。这个时候我们称函数复合为随机变量（向量、过程、等等，统称随机元）的分布 (distribution) ，对于随机变量的情况，就是我们熟知的概率分布函数啦！

呃，似乎还是没有用到积分……其实积分是被用来引入期望了，一个随机元的期望定义为

例如，对于一个离散型随机变量，设为一个简单函数，那么其期望为

也和熟知的离散型随机变量的期望定义是一致的。暂时不想举更多的例子了，于是一切要在此戛然而止了，篇幅也已经比较长了，后续的内容，大概要作为正式学习概率论的笔记的形式出现了吧。

概率与测度 (3)：概率模型

系列的前面两篇大致陈述了一下测度论方面的基础，由于这个学期有去旁听《概率论》这门课，所以主要还是按照课程进度来吧，不定期地把课程里一些有意思的内容抽取出来整理在这里。这次就说概率模型。

先从一个例子开始，比如一个盒子里放了 8 个黑球和 2 个白球，从盒子里随机拿一个球，问它是白球的概率是多少，大家都会不假思索地说，1/5 。的确，这似乎是很显然的，不过，实际上我们是用了一个模型来进行概率分析，但是由于这个情况实在太简单了，我们根本就没有注意到模型的存在性，但是换一个稍微简单的例子，要忽略模型“走捷径”有时候就会一下子想不清楚了。比如两个人各掷一个骰子，问 A 得到的点数比 B 大的概率。这个问题就比刚才那个问题要困难一些了。

最早人们在对这类概率问题进行数学抽象的时候，归纳出来的一种模型，现正称为古典概率模型。该模型包由一个包含有限个（设为）元素的样本空间组成，中的每一个元素称为一个基本事件，的任意一个子集是一个事件。所有基本事件的概率是相等的，即，而任意事件的概率即为该集合的元素个数乘以，换句话说：

也就是该事件集合的元素个数除以样本空间的总元素个数。对于第一个例子，我们可以这样建立模型：对每一个球编号，一共 1 到 10 号，设 8 号和 9 号是白球，其他的都是黑球，样本空间为 {抽到的是 1 号球、抽到的是 2 号球、……、抽到的是 10 号球} ，而“抽到白球”这个事件集合即 {抽到的是 9 号球、抽到的是 10 号球} ，简单计算立即得到 1/5 的概率。

对于第二个问题，我们用一个 tuple 来记两次掷骰子的结果，则整个样本空间集合为 {, , } 一共 36 个元素，要计算 A 的点数大于 B 的点数这个事件中基本事件的个数，只要暴力数一遍就好了（当然有更好的办法，例如先去掉相等的点数，然后利用对称性，但是这种具体的细节不是我们这里要关注的东西）。

心里有精确的模型存在的时候，就不至于“凭感觉”去想问题而导致各种混淆和错误了。不过古典概率模型实际上限制是比较大的，首先一个是各个基本事件的概率是一样的，这一点可以稍作修改得到稍微改进的版本。不过最主要的限制还在于样本空间必须是有限的这个问题上，在这里没有办法做直接推广，因为古典概率模型中事件的概率实际上就是把事件中包含的基本事件的概率全部加起来而得到的，但是如果集合的元素并不限制为有限个的话，求和式是不是有意义并且收敛就不一定能保证了。

除了古典概率模型之外呢，还有一个比较直观的模型叫做几何概率模型。它的样本空间为上的一个“可求体积”的图形；基本事件是该图形中的点，而基本事件的概率为零；事件则是该图形的“可求体积”的子图形，一个事件的概率通过如下公式计算：

其中表示样本空间的体积，而表示事件的体积。关于“可求体积”这个模糊的概念，我们待会再说。这里先举一个例子。比较有名的例子当属 Buffon’s needle 了，它有一个有趣的应用就是可以用来估计的值。这个例子虽然也不难，但是为了节省时间（好困…… ~_~），我们直接讲一个最简单直接的例子：在平面上有一个矩形，矩形里有一个圆，从矩形里任意选一个点，这个点落在圆内的概率是多少？这个问题正好就适合这里提到的几何概率模型——模型都不用建了，问题本身就已经建好了，比如，假设矩形是以原点为中心，边长为 2 的正方形，而圆是以原点为中心，半径为 1 的圆，那么根据刚才的公式，立即可以算出来概率为。

另一方面，我们知道（为什么？）具体试验所得到的频率是趋向于该事件的概率的。因此，我们可以通过做实验的方法来估算概率，从而反过来得到的数值。在这里我就纯粹用程序来模拟一下：

require 'open-uri'
 
EDGE_LEN = 1.2
 
def rand_ptr
    return [2*EDGE_LEN*rand-EDGE_LEN, 2*EDGE_LEN*rand-EDGE_LEN]
end
 
$rnd_org_nums = []
def rnd_org_rand_num
    if $rnd_org_nums.empty?
        puts "Getting new random numbers from random.org"
        $rnd_org_nums += open('http://www.random.org/decimal-fractions/?num=10000&dec=10&col=1&format=plain&rnd=new').
            read.split.map { |s| s.to_f }
    end
    return $rnd_org_nums.pop
end
def rnd_org_rand_ptr
    return [2*EDGE_LEN*rnd_org_rand_num-EDGE_LEN, 2*EDGE_LEN*rnd_org_rand_num-EDGE_LEN]
end
 
$dev_rnd_nums = []
INT32_MAX = 2**32
def dev_rnd_rand_num
    if $dev_rnd_nums.empty?
        puts "Getting new random numbers from /dev/urandom"
        $dev_rnd_nums += open('/dev/urandom').read(10000*4).unpack("L*").
            map { |i| i.to_f / INT32_MAX }
    end
    return $dev_rnd_nums.pop
end
def dev_rnd_rand_ptr
    return [2*EDGE_LEN*dev_rnd_rand_num-EDGE_LEN, 2*EDGE_LEN*dev_rnd_rand_num-EDGE_LEN]
end
 
def in_circle(ptr)
    ptr[0]*ptr[0] + ptr[1]*ptr[1] <= 1 ? 1 : 0
end
 
def find_freq(n)
    (1..n).map {
        #in_circle(dev_rnd_rand_ptr)
        in_circle(rand_ptr)
    }.inject(0) {|a,b| a+b}.to_f / n
end
 
pi = find_freq(50000)*(2*EDGE_LEN)*(2*EDGE_LEN)
puts "Pi = #{pi}"

其实代码不用这么长的，写了这么多是因为除了用 Ruby 自带的伪随机数生成器来随机之外，还尝试了 Linux kernel 附带的据说“随机性更好”的伪随机数生成器 /dev/urandom （如果直接用真随机的 /dev/random 的话，经常 block 住……）。另外还尝试了下 random.org 提供的真随机数服务来获取随机数——不过似乎很容易就超过每天的 quota 了。到底什么样的随机数“更加随机”嘛，我想下面这个呆伯特的漫画很能说明问题：

模拟的结果不是很理想，基本上保证能算对 3.1 这两位吧，也许重复次数增加会稍微好一点。不过传说曾经有人用 Buffon’s needle 模型（应该和这里差不多的）做实验数千次之后算到了的 7 位精度，听上去似乎是运气相当相当好才能达到这样的精度哦。不知道可否算一下：用这样的实验方法达到 7 位精度的概率是多少呢？

最后，再来说一下刚才提到的“可求体积”这个很不精准的概念，实际上看过前两次介绍或者对测度论有所了解的同学肯定已经明白是什么意思了，其实就是“可测”的意思。为了将这些不精确的地方精确化，将以前的那些概率模型归纳起来，建立一个严格的数学模型，作为现代概率论之父的 Andrey Kolmogorov 在测度论的基础上建立了公理化的现代概率模型。

在公理化体系里，一个概率空间由一个三元组组成，其中是样本空间，是的一个子集族，它必须是一个 -Algebra ，我们在最开始关于测度的介绍中也提到过，一个 -Algebra （或者称 -field ）是满足如下三条公理的一个集族：