算法基础练习题捏
技巧篇
技巧一:偏移量技巧
概览题目号
756(she型矩阵),1102, 1421
以下为习题区
题目区
题号756,蛇形矩阵
输入两个整数 n 和 m,输出一个 n行 m 列的矩阵,将数字 11 到 n×m按照回字蛇形填充至矩阵中。
具体矩阵形式可参考样例。
输入格式
输入共一行,包含两个整数 n 和 m。
输出格式
输出满足要求的矩阵。
矩阵占 n 行,每行包含 m 个空格隔开的整数。
数据范围
1≤n,m≤100
输入样例:
输出样例:
解释区
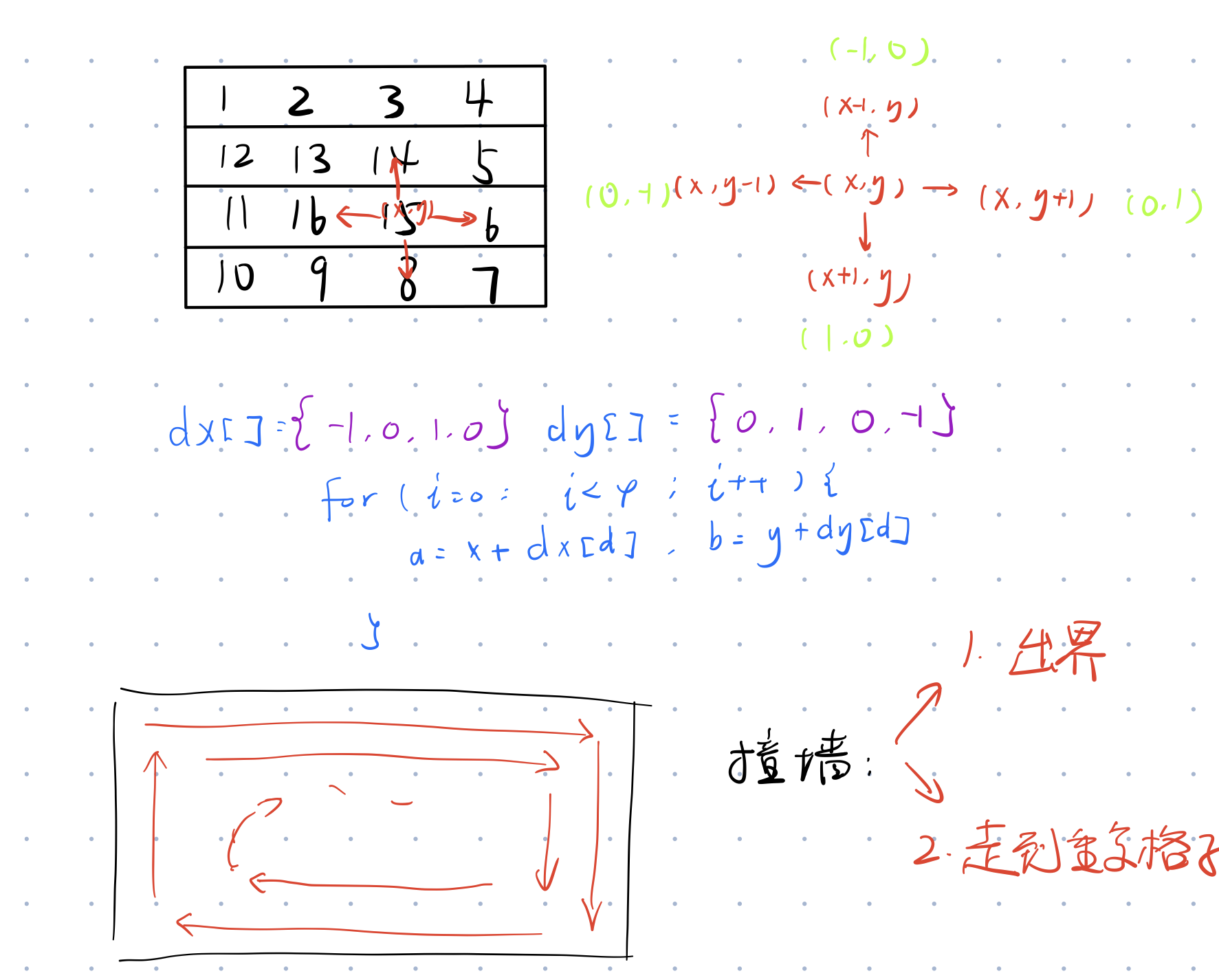
这里用到了一种特殊的处理方式,涉及到网格题目的时候,定义相邻格子,遍历这些格子的时候,比较笨的方法是用if判断,代码量长重复太多,这里介绍一种偏移量方法 ,可以循环枚举坐标。
代码区
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 #include <iostream> using namespace std;const int N = 110 ;int n, m;int q[N][N];int main () cin >> n >> m; int dx[] = {-1 , 0 , 1 , 0 }, dy[] = {0 , 1 , 0 , -1 }; int x = 0 , y = 0 , d = 1 ; for (int i = 1 ; i <= n*m ;i++){ q[x][y] = i; int a = x + dx[d], b = y + dy[d]; if (a < 0 || a >= n || b < 0 || b >= m || q[a][b] ) { d = (d+1 ) % 4 ; a = x + dx[d], b = y + dy[d]; } x = a, y = b; } for (int i =0 ; i < n ; i ++){ for (int j = 0 ; j < m; j ++ ) cout << q[i][j] << ' ' ; cout << endl; } return 0 ; }
同样小技巧
1102. 移动骑士 - AcWing题库
1421. 威斯康星方形牧场 - AcWing题库
基础算法篇
二分
解释区
然后就是个人习惯吧,个人比较喜欢把所求的设成1对应边界,比如 if( f(mid) < x ) l = mid + 1
所求的目标值每次都在选的区间中,这样递归下去,当区间长度为1时。自然就是正确答案了捏
模板区
注意:模板一定保证有解,就是会得到一个数,要么就是边界,要么就是最接近符合边界条件的数
二分模板一共有两个,分别适用于不同情况。
版本1
C++ 代码模板:
1 2 3 4 5 6 7 8 9 10 int bsearch_1 (int l, int r) while (l < r) { int mid = l + r >> 1 ; if (check (mid)) r = mid; else l = mid + 1 ; } return l; }
版本2
C++ 代码模板:
1 2 3 4 5 6 7 8 9 10 int bsearch_2 (int l, int r) while (l < r) { int mid = l + r + 1 >> 1 ; if (check (mid)) l = mid; else r = mid - 1 ; } return l; }
题目区
67. 数字在排序数组中出现的次数 - AcWing题库
789. 数的范围 - AcWing题库
790. 数的三次方根 - AcWing题库
以789和790为例
789.数的范围
给定一个按照升序排列的长度为 n 的整数数组,以及 q 个查询。
对于每个查询,返回一个元素 k 的起始位置和终止位置(位置从 00 开始计数)。
如果数组中不存在该元素,则返回 -1 -1。
输入格式
第一行包含整数n 和 q,表示数组长度和询问个数。
第二行包含 n 个整数(均在 1∼100001∼10000 范围内),表示完整数组。
接下来 q 行,每行包含一个整数 k,表示一个询问元素。
输出格式
共 q 行,每行包含两个整数,表示所求元素的起始位置和终止位置。
如果数组中不存在该元素,则返回 -1 -1。
数据范围
1≤n≤1000001≤n≤100000
输入样例 :
输出样例 :
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 #include <iostream> using namespace std;const int N = 100010 ;int n, m;int q[N];int main (void ) scanf ("%d%d" , &n, &m); for (int i =0 ; i < n; i++) scanf ("%d" , &q[i]); while ( m-- ){ int x; scanf ("%d" , &x); int l = 0 , r = n - 1 ; while (l < r){ int mid = l + r >> 1 ; if (q[mid] < x) l = mid + 1 ; else r = mid; } if (q[l] != x){ cout << -1 << ' ' << -1 << endl; continue ; } cout << l << ' ' ; l=0 , r = n - 1 ; while ( l < r){ int mid = l + r + 1 >>1 ; if (q[mid] <= x) l = mid; else r = mid - 1 ; } cout << l << endl; } return 0 ; }
790.数的三次方根
本题是实数二分,注意 >> 1位运算换成 /2,以及更新的时候是 l = mid or r = mid,没有+1,-1这种
给定一个浮点数 n,求它的三次方根。
输入格式
共一行,包含一个浮点数 n。
输出格式
共一行,包含一个浮点数,表示问题的解。
注意,结果保留 66 位小数。
数据范围
−10000≤n≤10000−10000≤n≤10000
输入样例 :
输出样例 :
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 #include <iostream> using namespace std;int main (void ) double x; cin >> x; double l = -10000 , r = 10000 ; while ( r - l > 1e-8 ){ double mid = (l + r)/2 ; if (mid*mid*mid < x ) l = mid; else r = mid; } printf ("%.6lf" , l); }
快排
解释区
模板区
AcWing 785. 快速排序算法的证明与边界分析 - AcWing
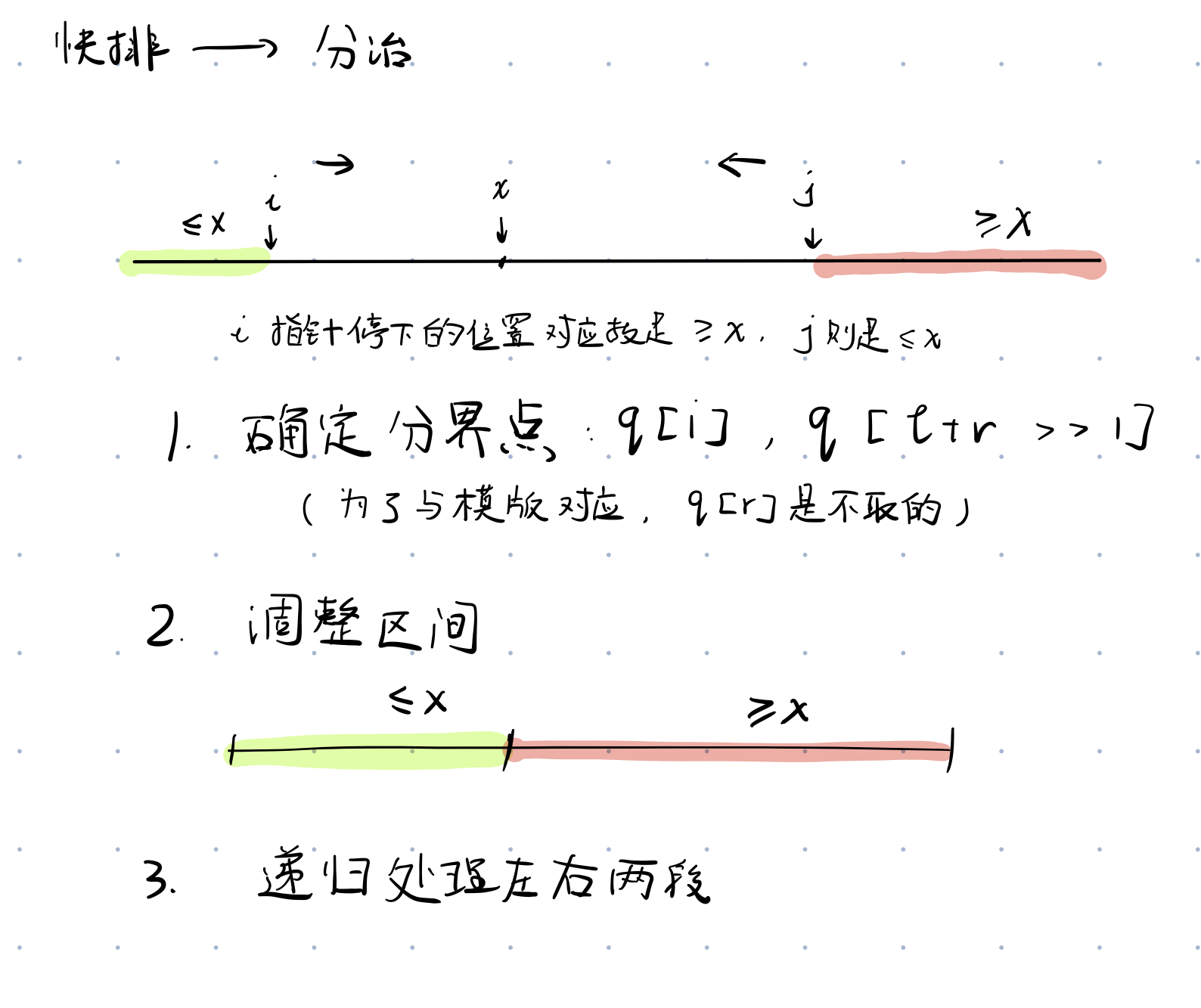
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 void quick_sort (int q[], int l, int r) if (l >= r) return ; int i = l - 1 , j = r + 1 , x = q[l + r >> 1 ]; while (i < j) { do i++; while (q[i] < x); do j--; while (q[j] > x); if (i < j) swap (q[i], q[j]); } quick_sort (q, l, j), quick_sort (q, j + 1 , r); }
补充一下捏 :
终止的情况 有两种,i = j 和 i,j 错开,也就是i = j + 1。可以这么想,i 停下的位置,无非就两种情况,=x或者>x,最终停下的位置是前者可能会造成i = j(不是一定的捏),后者则一定会造成i,j错位。
e.g.:22222(i=j),222222(i,j错位),31462(i,j错位)
无限划分 的情况,当x = q[l] or q[l + r >> 1]时,j的取值范围为[l..r-1],不会造成数组越界和无限划分,但是如果x = q[r],则会造成划分为n,0的可能,形成无限划分。
题目区
785. 快速排序 - AcWing题库
快速查找
解释区
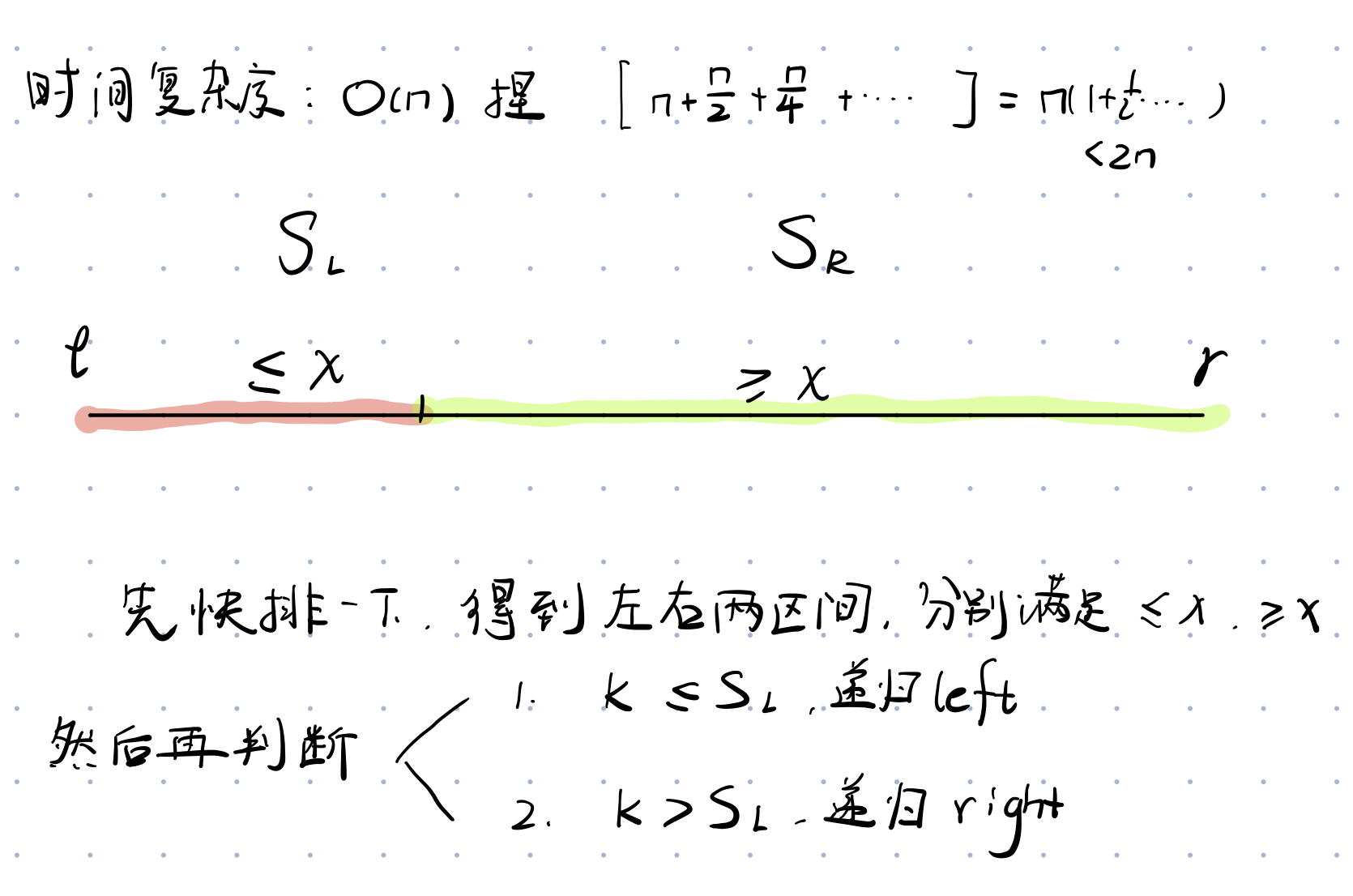
快速查找是利用了快排的部分有序(划分筛选区间)和二分的思想。
模板区
这里是利用下标的大小来判断的
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 int quick_select (int l, int r) if (l == r) return q[l]; int i = l - 1 , j = r + 1 , x = q[l + r >> 1 ]; while (i < j) { do i ++ ; while (q[i] < x); do j -- ; while (q[j] > x); if (i < j) swap (q[i], q[j]); } if (k <= j) return quick_select (l, j); return quick_select (j + 1 , r); }
题目区
786. 第k个数 - AcWing题库
P1138 第k小整数 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
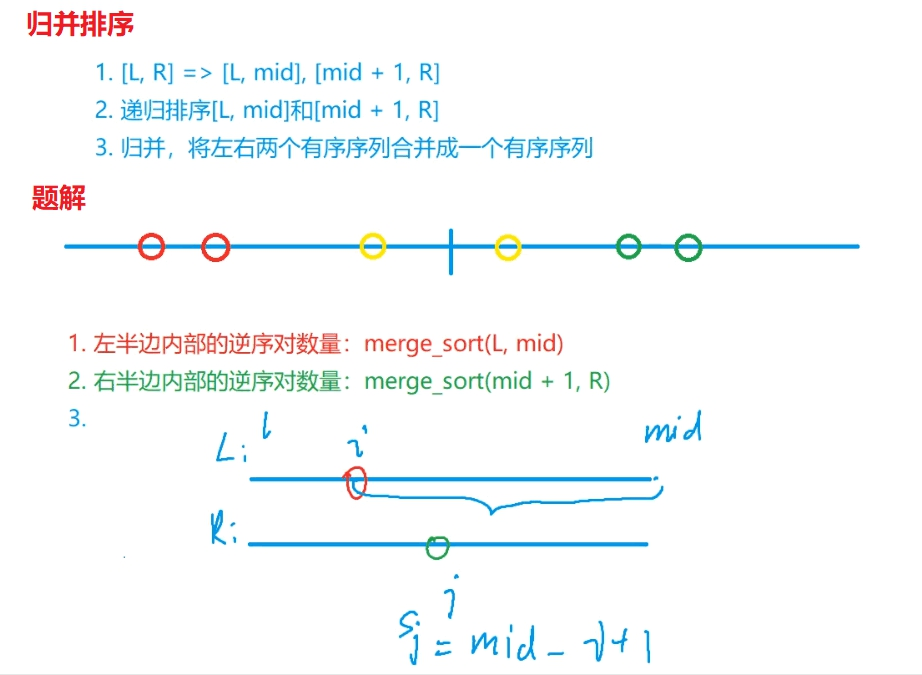
归并排序
解释区
模板区
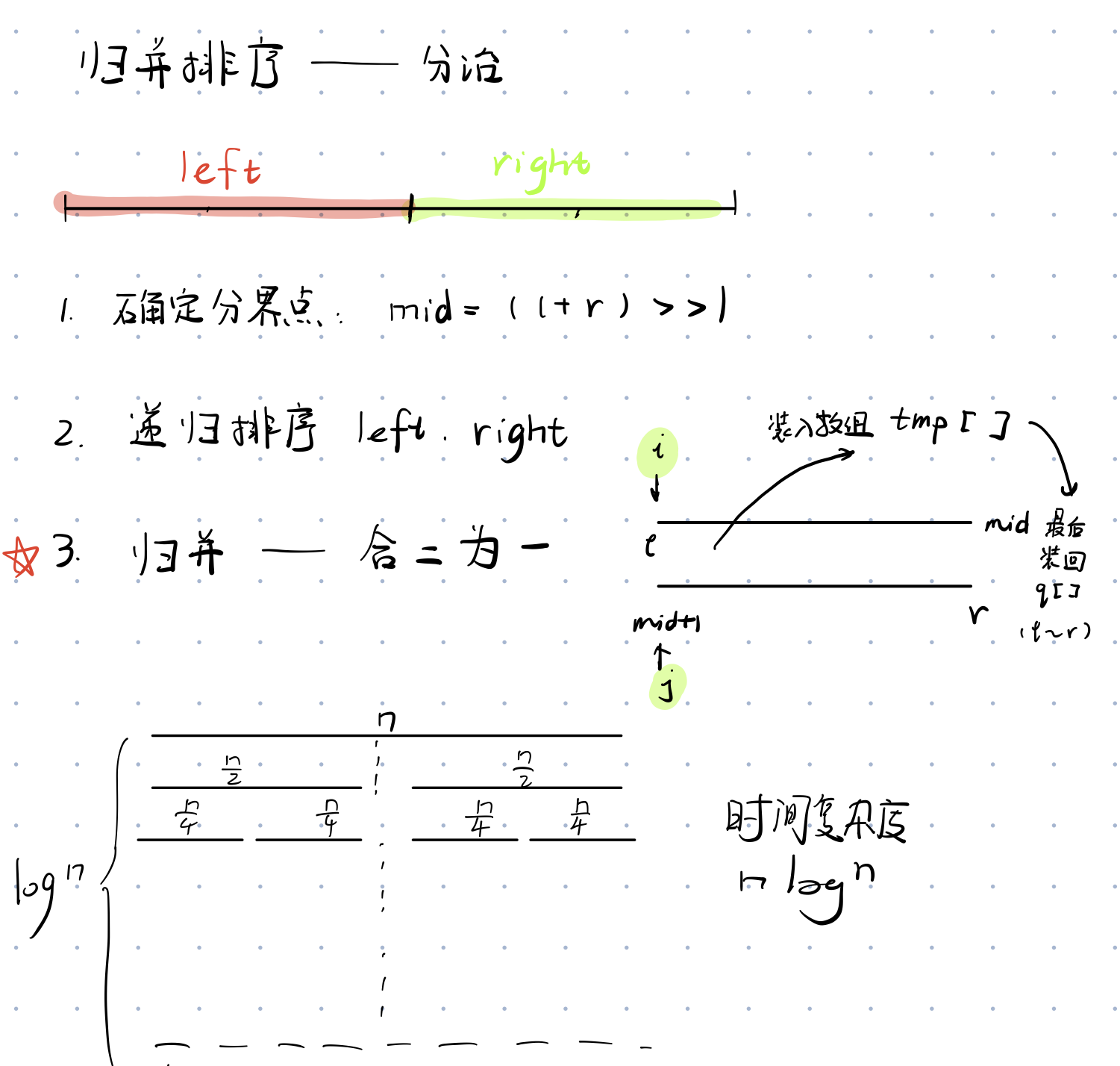
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 void merge_sort (int q[], int l, int r) if (l >= r) return ; int mid = (l + r) >> 1 ; merge_sort (q,l,mid), merge_sort (q, mid + 1 , r); int k = 0 , i = l, j = mid + 1 ; while (i <= mid && j <= r) if (q[i] <= q[j]) tmp[k++] = q[i++]; else tmp[k++] = q[j++]; while (i <= mid) tmp[k++] = q[i++]; while (j <= r) tmp[k++] = q[j++]; for (int i = l, j = 0 ; i <= r ; i++, j++) q[i] = tmp[j]; }
题目区
787. 归并排序 - AcWing题库
788. 逆序对的数量 - AcWing题库
逆序对那题,其实也是说一种划分区间递归的操作,对于某个数字的逆序对数来说,只要看这个数字之前的元素中有多少是大于这数字的,于是原区间所有逆序对数可以分为,前半区间内的逆序对总数,后半区间内的逆序对总数,和后半区间对于前半的逆序对总数。这个划分正好可以用归并排序实现,具体来说,只要在合并操作中进行逆序对的计数就可了(因为前半和后半的逆序数已经统计过了)。
高精度
解释区
模板区
1.大数是逆序存到数组里
1 2 vector<int > A; for (int i = a.size () - 1 ; i >= 0 ; i--) A.push_back (a[i] - '0' );
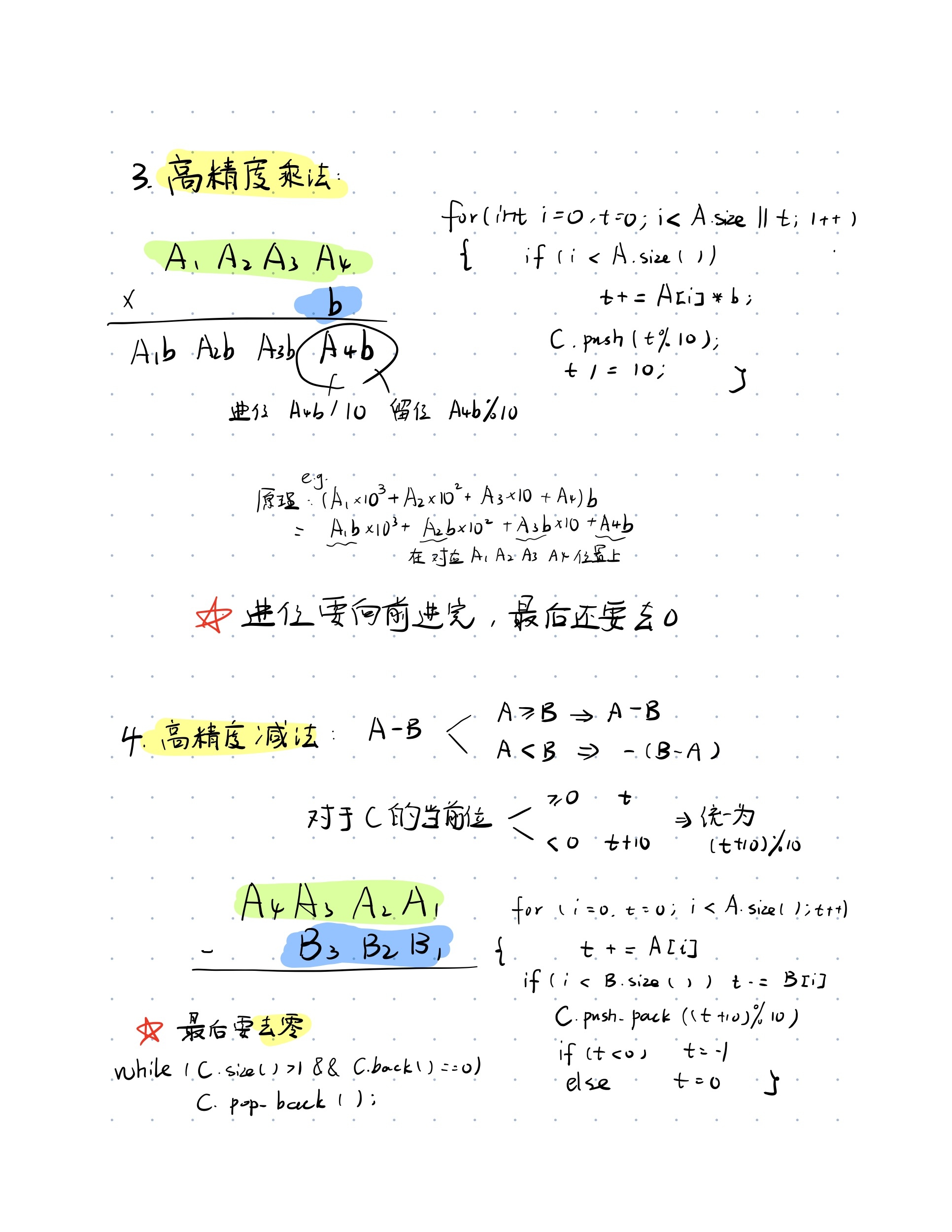
2.对于加法和乘法而言,要考虑留位和进位的处理
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 for (int i = 0 ;i < A.size () || i < B.size (); i ++){ if (i < A.size ()) t += A[i]; if (i < B.size ()) t += B[i]; C.push_back (t%10 ); t /= 10 ; } if (t) C.push_back (1 );for (int i = 0 , t = 0 ; i < A.size () || t; i++){ if (i < A.size ()) t += A[i]*b; C.push_back ( t%10 ); t /= 10 ; } while (C.size () > 1 && C.back () == 0 ) C.pop_back ();
3.对减法考虑的因素比较多
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 bool cmp (vector<int > &A, vector<int > &B) if (A.size () != B.size ()) return A.size () > B.size (); for (int i = A.size () - 1 ; i>=0 ; i--) if (A[i] != B[i]) return A[i] > B[i]; return true ; } vector<int > subtraction (vector<int > & A, vector<int > & B) { vector<int > C; for (int i = 0 , t = 0 ; i < A.size (); i++){ t += A[i]; if (i < B.size ()) t -= B[i]; C.push_back ((t+10 )%10 ); if (t < 0 ) t = -1 ; else t = 0 ; } while (C.size () > 1 && C.back () == 0 ) C.pop_back (); return C; }
4.除法
1 2 3 4 5 6 7 for (int i = A.size () - 1 ; i >= 0 ; i--){ r = (10 *r + A[i]); C.push_back ( r / b); r = r % b; } reverse (C.begin (), C.end ());while (C.size () > 1 && C.back () == 0 ) C.pop_back ();
5.乘法,除法,减法均要考虑去0
题目区
791. 高精度加法 - AcWing题库
792. 高精度减法 - AcWing题库
793. 高精度乘法 - AcWing题库
794. 高精度除法 - AcWing题库
前缀和
解释区
模板区
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 #include <iostream> using namespace std;const int N = 1010 ;int a[N][N], s[N][N]; int main (void ) int m,n,q; scanf ("%d%d%d" , &n,&m,&q); for (int i = 1 ; i <= n; i++) for (int j = 1 ; j <= m; j++) scanf ("%d" , &a[i][j]); for (int i = 1 ; i <= n; i++) for (int j = 1 ; j <= m; j++) s[i][j] = s[i-1 ][j] + s[i][j-1 ] -s[i-1 ][j-1 ] + a[i][j]; while (q--){ int x1,y1,x2,y2; scanf ("%d%d%d%d" ,&x1,&y1,&x2,&y2); printf ("%d\n" , s[x2][y2] - s[x1-1 ][y2] - s[x2][y1 -1 ] + s[x1-1 ][y1- 1 ]); } return 0 ; }
题目区
796. 子矩阵的和 - AcWing题库
99. 激光炸弹 - AcWing题库
AcWing 121. 赶牛入圈 - AcWing
区间合并
解释区
模板区
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 typedef pair<int , int > PII;vector<PII> segs; void merge (vector<PII> &segs) vector<PII> res; sort (segs.begin (), segs.end ()); int st = -2e9 , ed = -2e9 ; for (auto seg : segs){ if (ed < seg.first){ if (st != -2e9 ) res.push_back ({st,ed}); st = seg.first, ed = seg.second; } else ed = max (ed, seg.second); } if (st != -2e9 ) res.push_back ({st,ed}); segs = res; }
题目区
803. 区间合并 - AcWing题库
离散化
解释区
模板区
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 #include <iostream> #include <vector> #include <algorithm> using namespace std;typedef pair<int , int > PII;const int N = 300010 ;vector<PII> add, query; vector<int > alls; int a[N], s[N];vector<int >::iterator unique (vector<int > &a) int j = 0 ; for (int i = 0 ; i < a.size (); i ++ ) if (!i || a[i] != a[i - 1 ]) a[j ++ ] = a[i]; return a.begin () + j; } int find (int x) int l = 0 , r = alls.size () - 1 ; while (l < r){ int mid = l + r >> 1 ; if (alls[mid] >= x) r = mid; else l = mid + 1 ; } return r + 1 ; } int main (void ) int n,m; cin >> n >> m; for (int i = 0 ; i < n; i++){ int x, c; cin >> x >> c; add.push_back ({x, c}); alls.push_back (x); } for (int i = 0 ; i < m; i++){ int l, r; cin >> l >> r; query.push_back ({l, r}); alls.push_back (l); alls.push_back (r); } sort (alls.begin (), alls.end ()); alls.erase (unique (alls.begin (), alls.end ()), alls.end ()); for (auto item : add){ int x = find (item.first); a[x] += item.second; } for (int i = 1 ; i <= alls.size (); i++) s[i] = s[i-1 ] + a[i]; for (auto item : query){ int l = find (item.first), r = find (item.second); cout << s[r] - s[l - 1 ] << endl; } return 0 ; }
题目区
802. 区间和 - AcWing题库
103. 电影 - AcWing题库
121. 赶牛入圈 - AcWing题库
电影代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 #include <iostream> #include <vector> #include <algorithm> using namespace std;const int N = 200010 ;vector<int > alls; int lan[N]; int a[N],b[N]; int cont[3 *N];int find (int x) int l = 0 , r = alls.size () - 1 ; while (l < r){ int mid = l + r >>1 ; if (alls[mid] >= x) r = mid; else l = mid + 1 ; } return r; } int main (void ) int n,m; int tot = 0 ; cin >> n; for (int i = 0 ; i < n; i++){ scanf ("%d" , &lan[i]); alls.push_back (lan[i]); } cin >> m; for (int i = 0 ; i < m ; i++){ scanf ("%d" , &a[i]); alls.push_back (a[i]); } for (int i = 0 ; i < m; i++){ scanf ("%d" , &b[i]); alls.push_back (b[i]); } int j = 0 ; sort (alls.begin (), alls.end ()); for (int i = 0 ; i < alls.size (); i++) if ( (i==0 ) || alls[i] != alls[i-1 ] ) alls[j++] = alls[i]; alls.erase (alls.begin ()+j, alls.end ()); for (int i = 0 ; i <n; i++) cont[find (lan[i])]++; int an0,anx,any; an0 = anx =any = 0 ; for (int i = 0 ; i < m ;i++){ if (cont[find (a[i])] > anx ||( cont[find (a[i])] == anx && cont[find (b[i])] > any) ) an0 = i, anx = cont[find (a[i])],any = cont[find (b[i])]; } cout << an0+1 ; return 0 ; }
赶牛入圈解释
很显然,本题草的坐标X,Y范围是1-10000,也就是一共
然后看题目所求的是畜栏的最小边长,通过y总的分析可知,最后答案的点一定是在边界上的,由此可以利用离散化后的点求二维前缀和,再通过二分答案判断选取最小的边长。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 #include <iostream> #include <vector> #include <algorithm> using namespace std;typedef pair<int ,int >PII;const int N=1010 ;int n,c;int sum[N][N];PII points[N]; vector<int >num; int dis (int x) int l=0 ,r=num.size ()-1 ; while (l<r){ int mid=(l+r)>>1 ; if (num[mid]>=x) r=mid; else l=mid+1 ; } return r; } int check (int len) for (int x1=1 ,x2=1 ;x2<num.size ();x2++){ while (num[x2]+1 -num[x1]>len) x1++; for (int y1=1 ,y2=1 ;y2<num.size ();y2++){ while (num[y2]+1 -num[y1]>len) y1++; if (sum[x2][y2]-sum[x1-1 ][y2]-sum[x2][y1-1 ]+sum[x1-1 ][y1-1 ]>=c) return 1 ; } } return 0 ; } int main () cin>>c>>n; num.push_back (0 ); for (int i=0 ;i<n;i++){ int x,y; cin>>x>>y; points[i]={x,y}; num.push_back (x); num.push_back (y); } sort (num.begin (),num.end ()); num.erase (unique (num.begin (),num.end ()),num.end ()); for (int i=0 ;i<n;i++){ int x=dis (points[i].first); int y=dis (points[i].second); sum[x][y]++; } for (int i=1 ;i<num.size ();i++){ for (int j=1 ;j<num.size ();j++){ sum[i][j]+=sum[i-1 ][j]+sum[i][j-1 ]-sum[i-1 ][j-1 ]; } } int l=1 ,r=10000 ; while (l<r){ int mid=(l+r)>>1 ; if (check (mid)) r=mid; else l=mid+1 ; } cout<<r<<endl; return 0 ; }




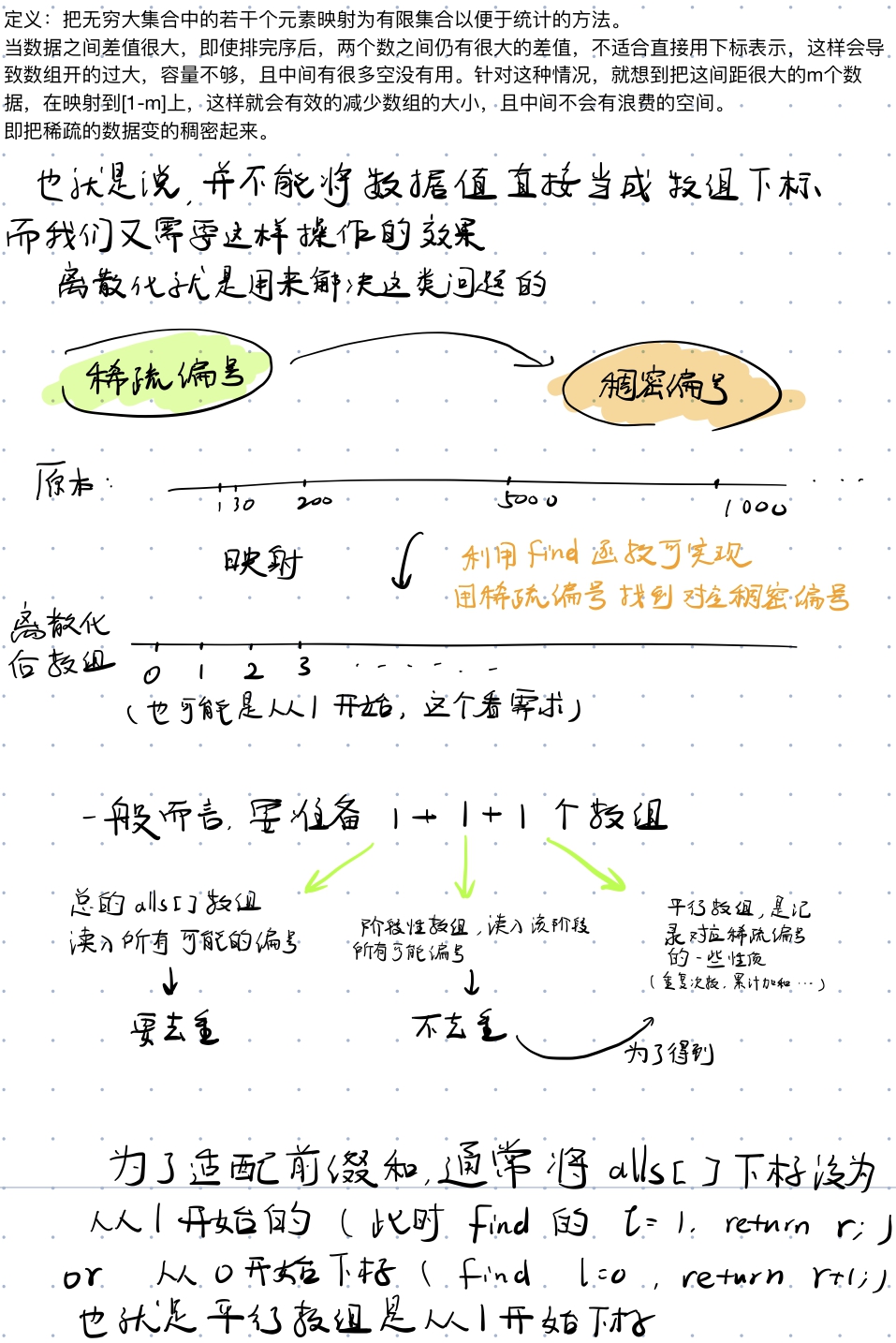
个坐标,而草的个数N只有最多500个,如果直接开
这么大的数组肯定是不能接受的,因此要采取离散化。











