FFT的详解
背景知识
-
Fourier Series 指数形式
-
DFS : cofficient -> value
-
DFS的矩阵形式(Fourier matrix)
引入FFT
FFT可以理解为快速计算Fourier matrix(Discrete Fourier matrix)的一种算法,其本质是多项式求值算法。
ps:而其逆也就是IFFT,是解决插值问题。
为啥 计算Fourier matrix times c 和 多项式求值 关联起来了?
以下为Fourier matrix
和范德蒙德矩阵其实是一样的!
Fourier级数的指数展开,和多项式其实是差不多的,离散的指数展开,就相当于n个n次多项式,每一个多项式的未知数均是x^n=1的根
进而可以将DFS转换为本质的polynomial求值问题
polynomial求值
Part1
先来一个Big picture
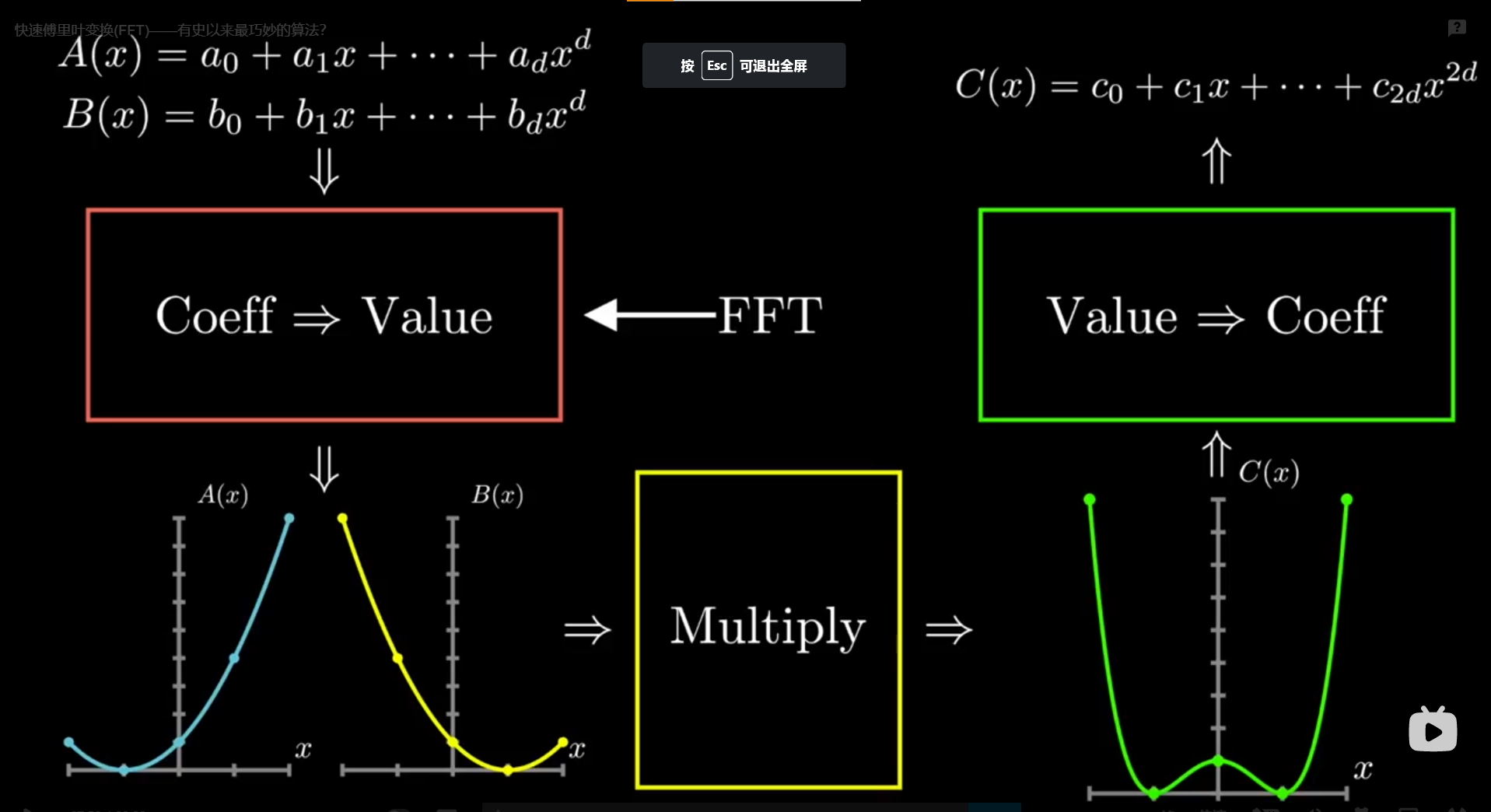
🆗,那么接下来我们首先关注coeff ->value,也就是求值部分,FFT大放光彩的地方
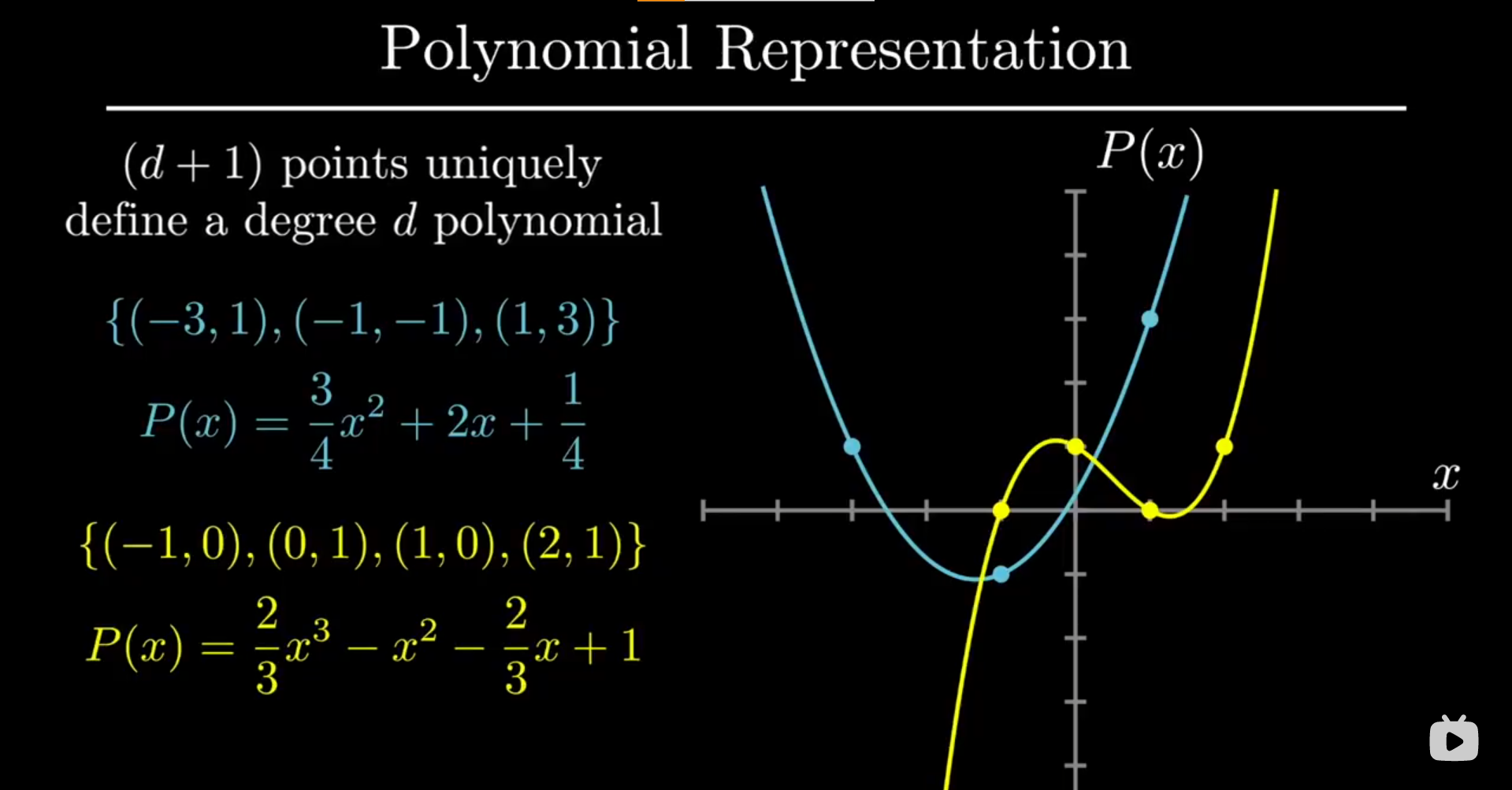
对于多项式,不仅有系数表示,还有点值表示

系数表示
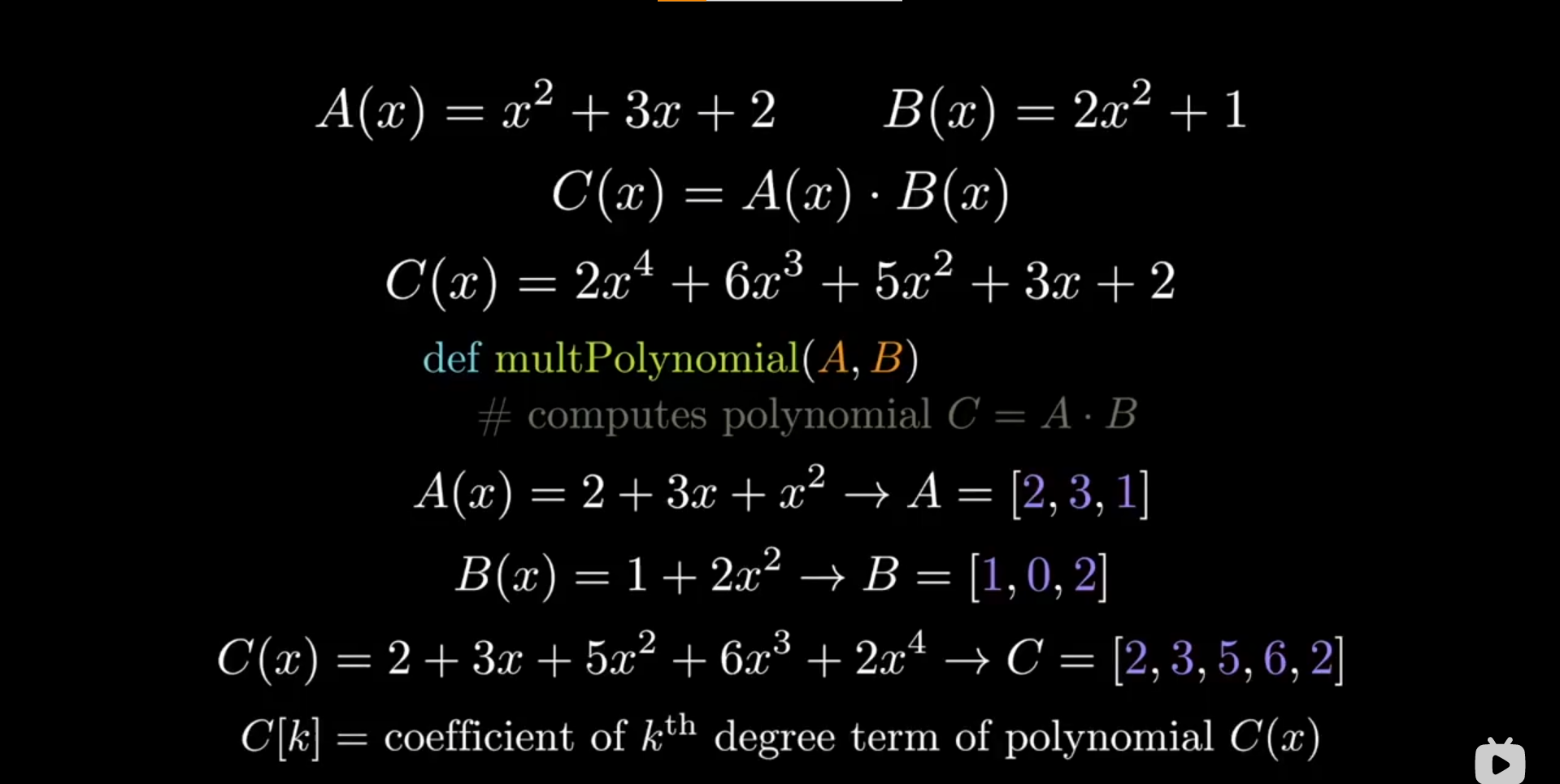
点值表示
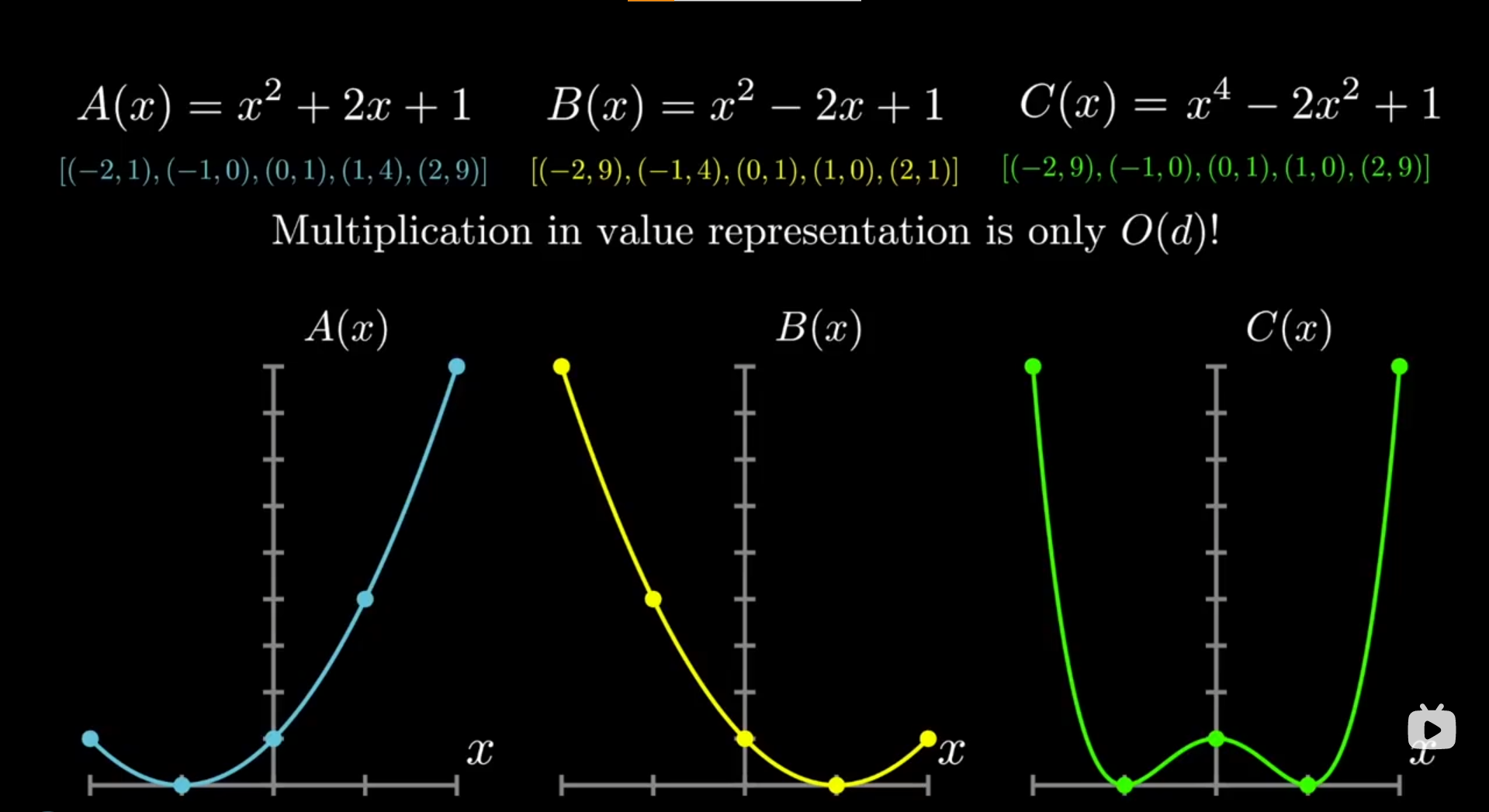
点值表示下的多项式乘法:O(n),对应函数值相乘即可
点值表示是唯一确定多项式的

系数表示和点值表示的整体对比

FFT采取的是点值表示
那么从函数本身的奇偶性,就不难发现可以简化
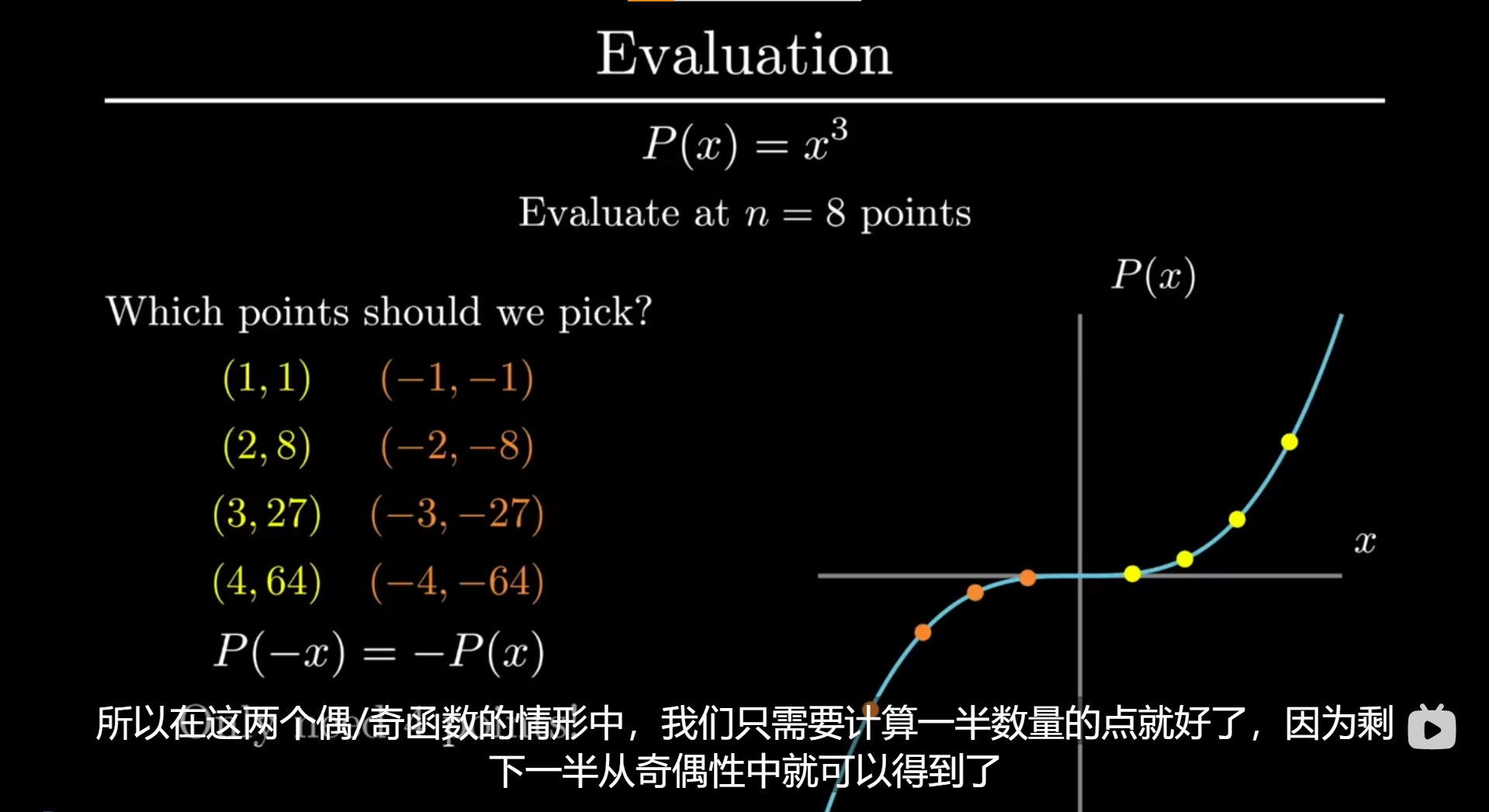
根据上面的灵感,可以把多项式分为奇/偶函数两部分,这样分解的好处是
- 对于一对相反数计算函数值时,只要计算其中一个
- 同时,我们把两个部分看作x^2的函数,P_e和P_o的阶数都降到了2,比原来的5阶求值简化了太多(5是n-1阶[取了6个点],P_e和P_o的阶数是n/2-1)

拓展到n-1阶多项式,我们要取n个点进行求值,也可以利用同样的思路,进而将问题简化为在n/2个点对n/2-1阶多项式的求值问题

小结

PS:由于前置的条件是n=2^k,也就是FFT处理2^k规模问题,引入次数界来扩展次数
Part2
通过上述分析,我们得到了一个极好的递归思路,但如果想对子问题应用同样的方法,那么对应的点
都还要满足是均分的相反数的性质,也就是n/2个点中,两个n/4部分互为相反数。
通过对傅里叶矩阵的思考,也不难得出我们所追寻的xi应该是-----复数单位根。
不难通过图像(or代数)直观感受当问题规模减半时,新的点之间的对称关系
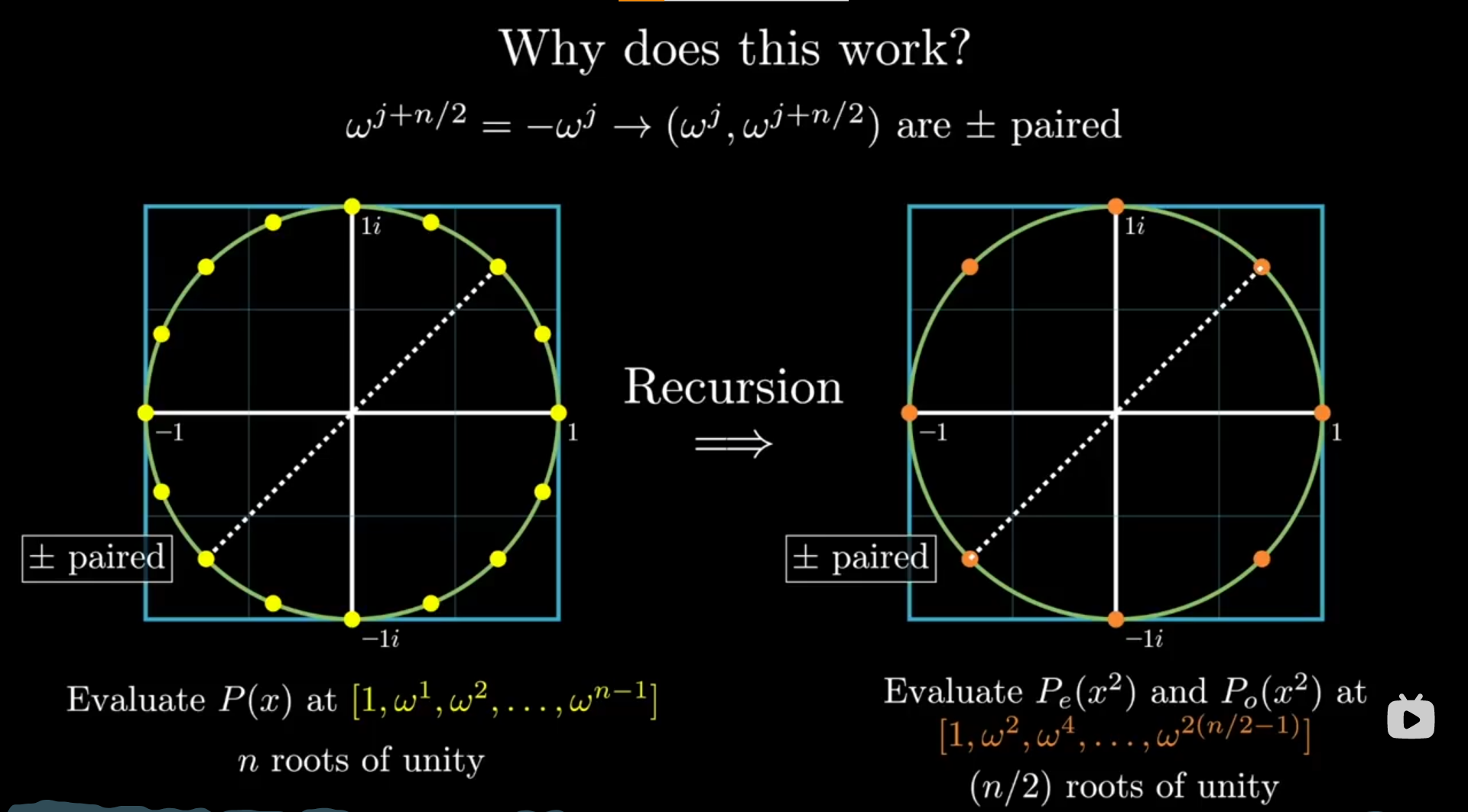
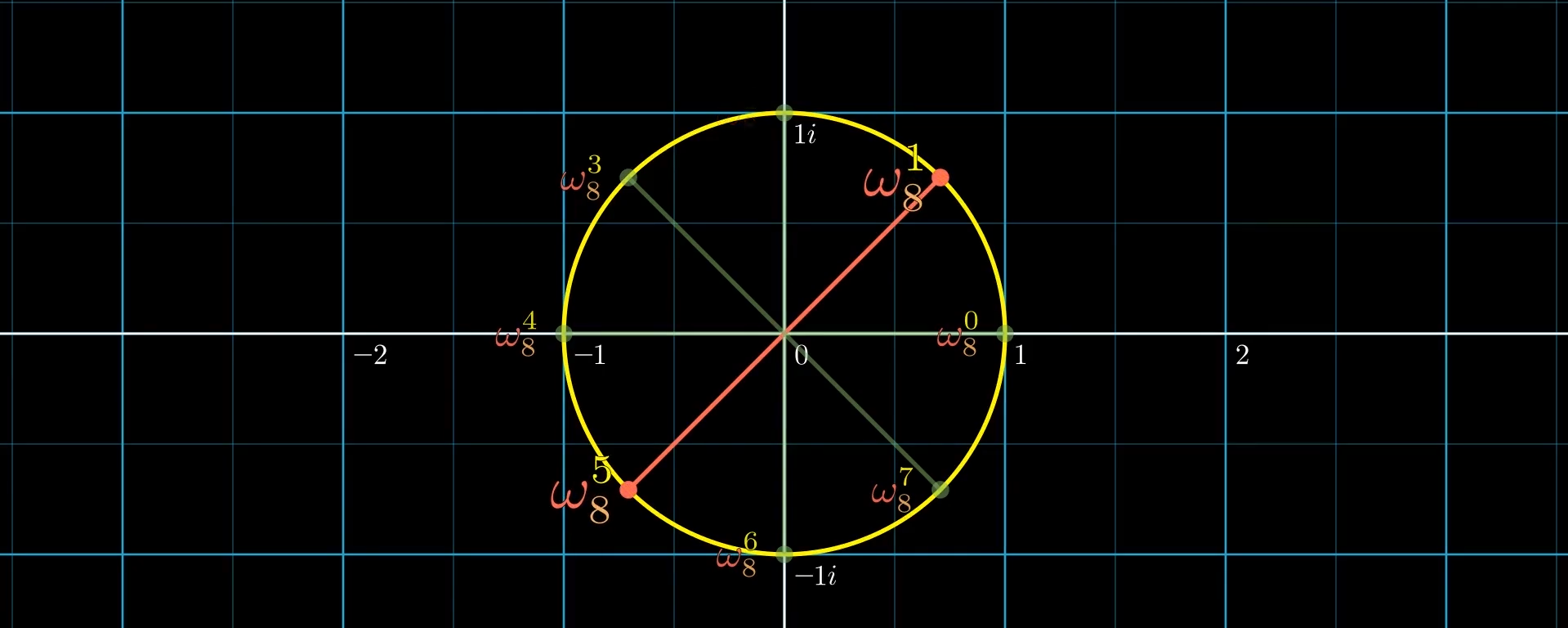
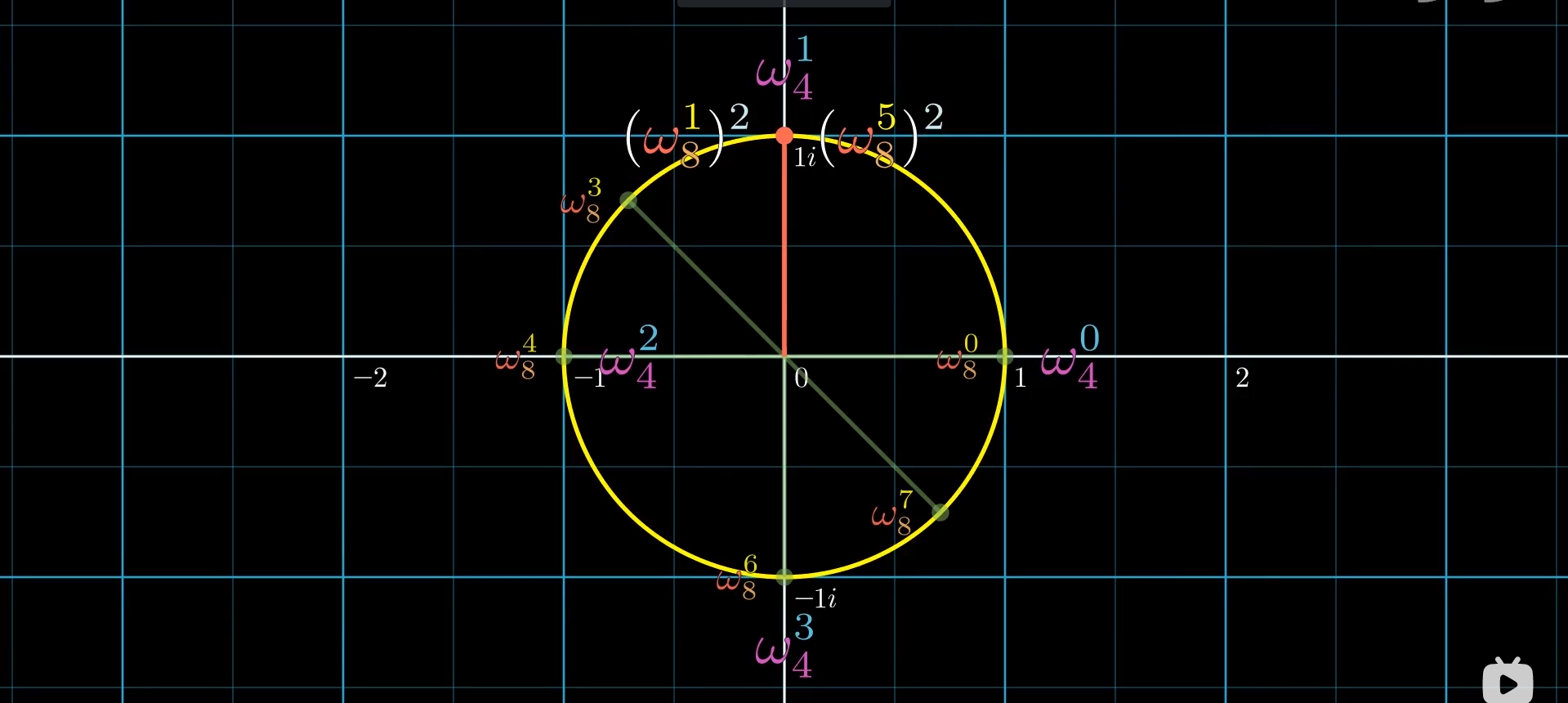
复数单位根的三个引理(性质)

Part3
接下来将多项式求值与复数单位根结合,得到完整的FFT
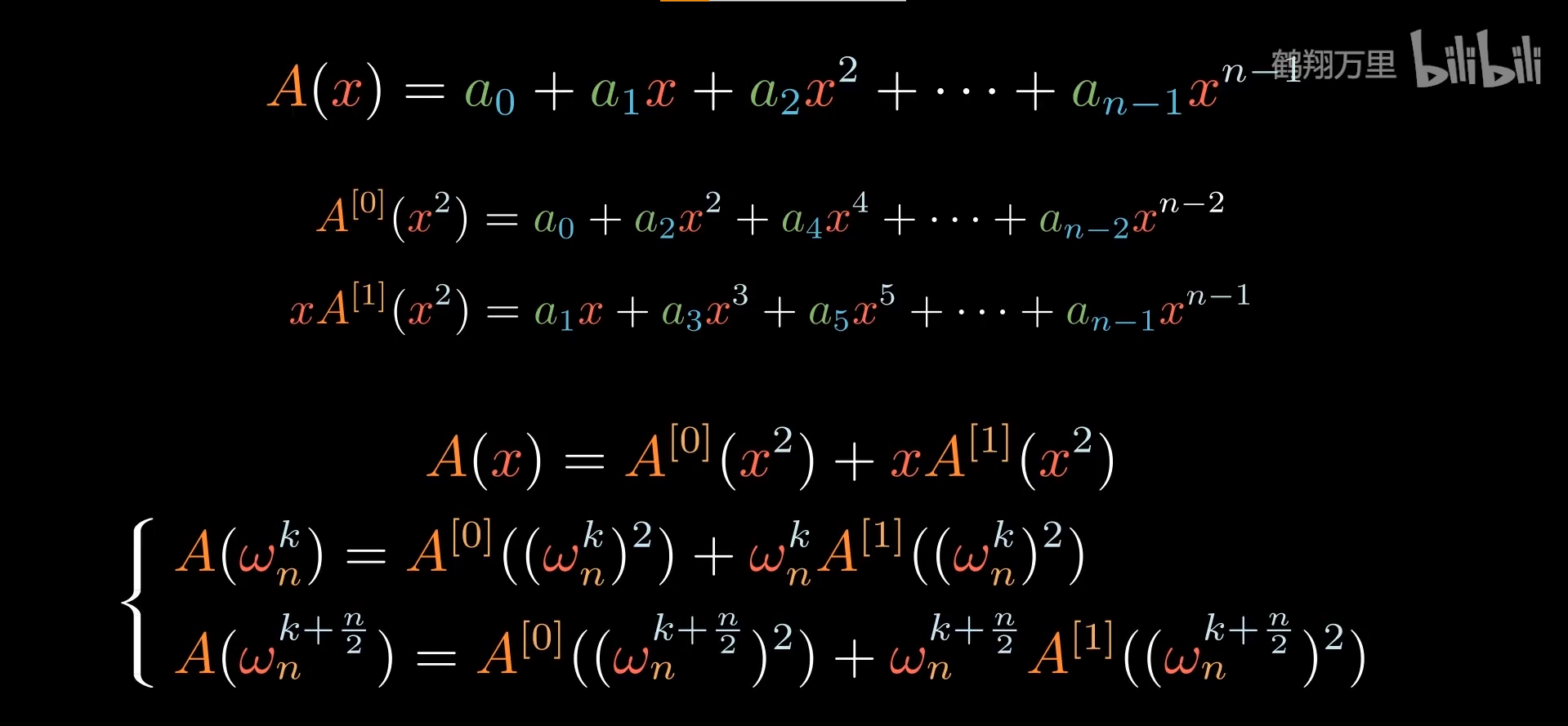
带入化简得
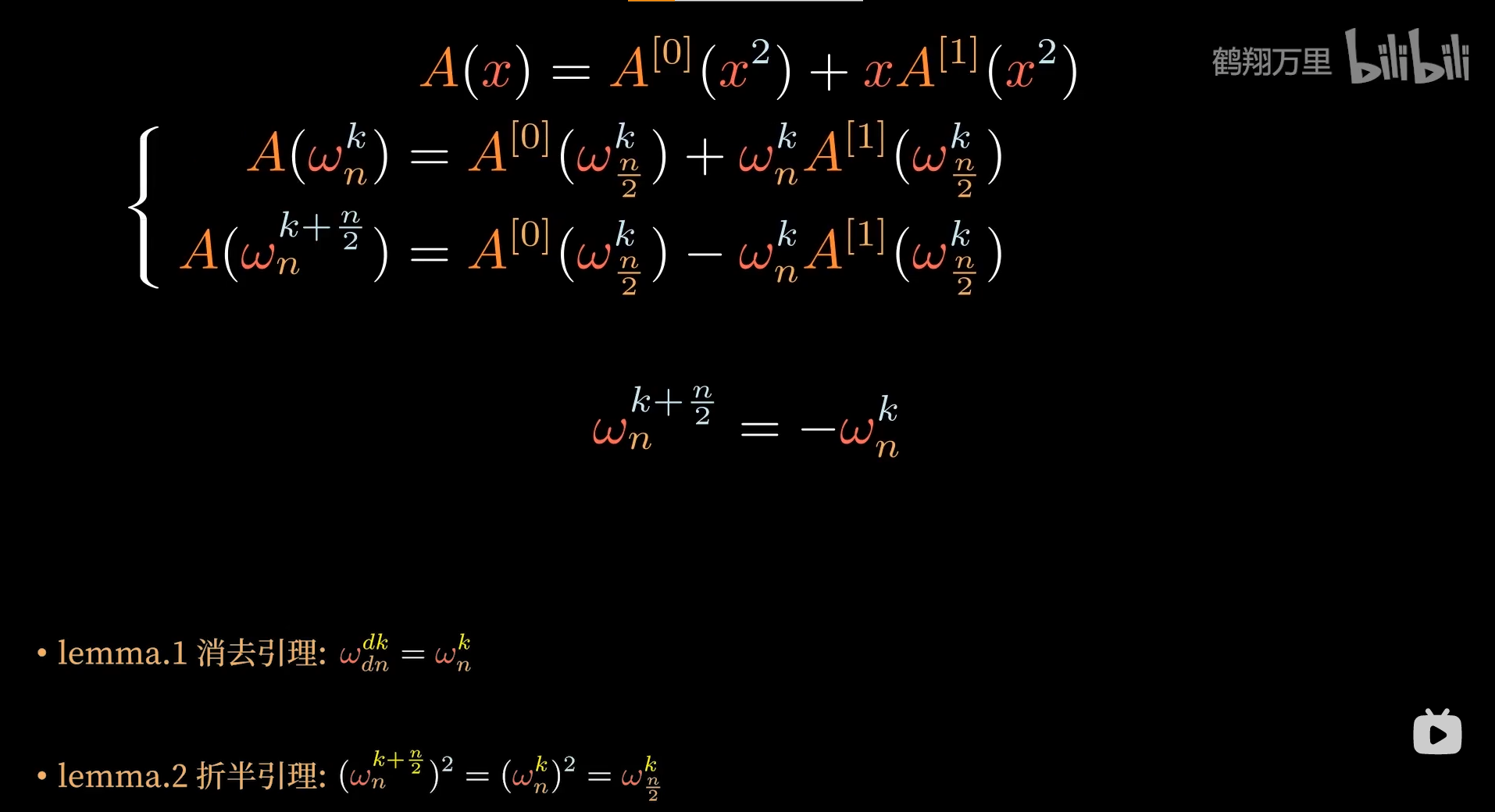
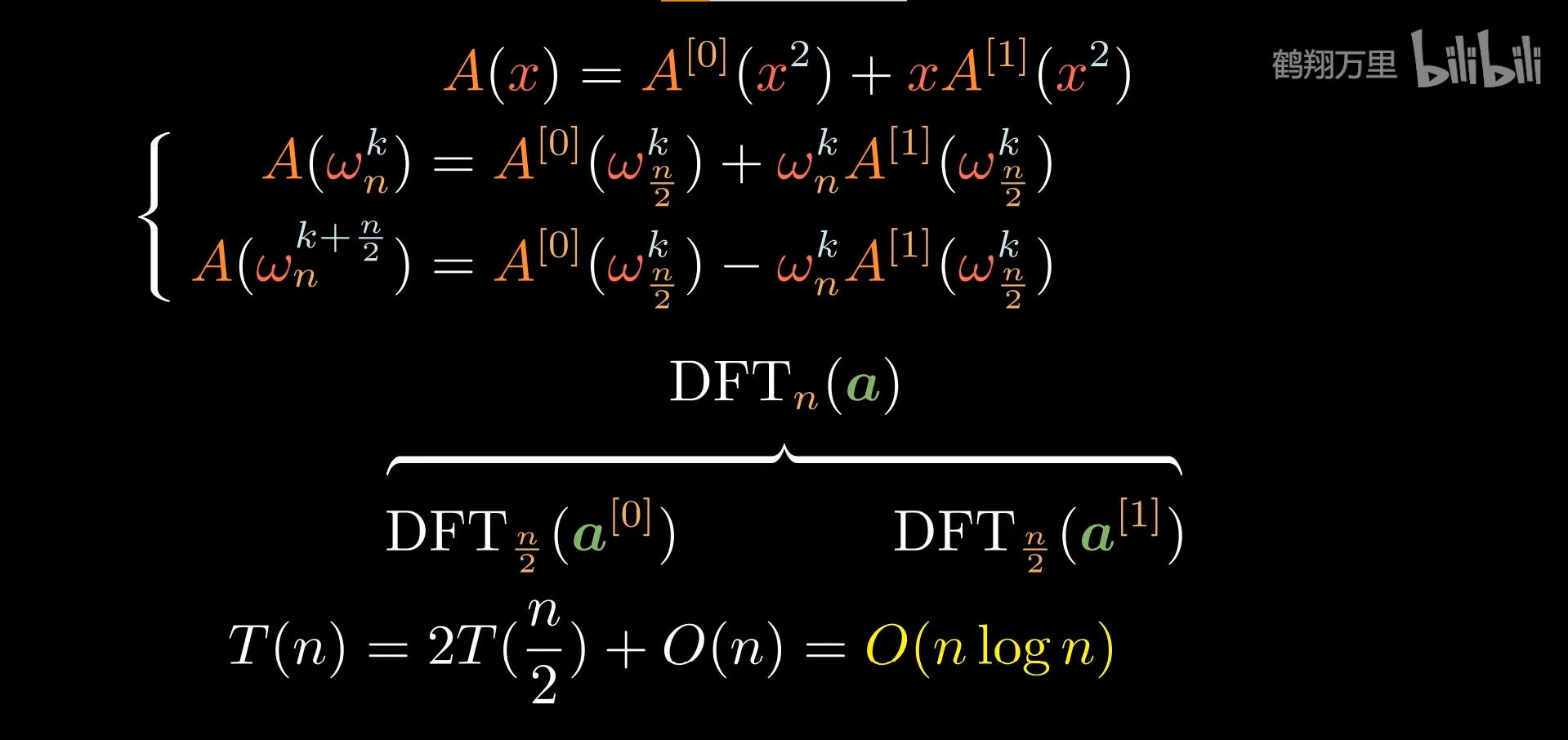
Part4
递归代码
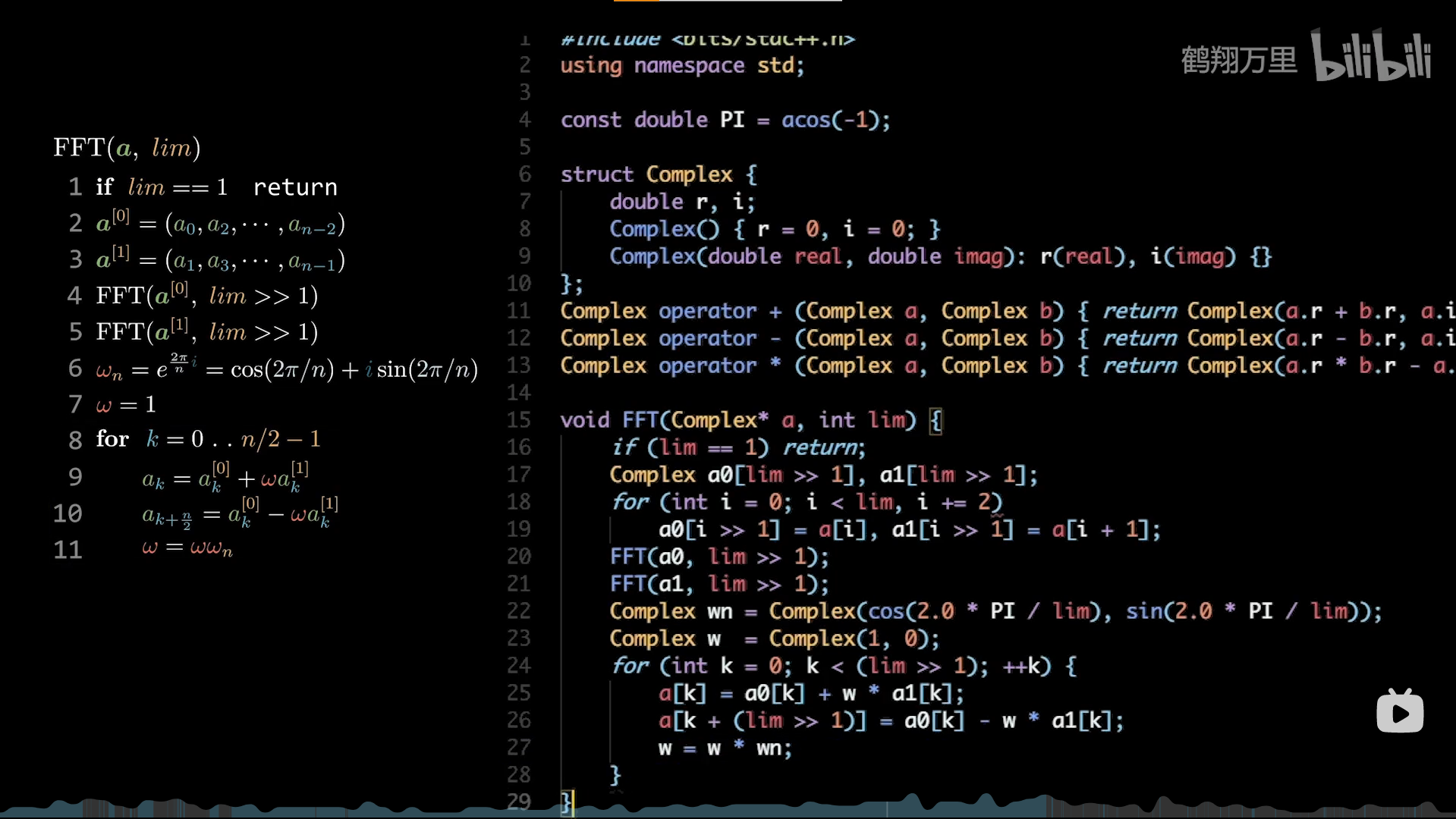
高效实现
🦋操作

迭代实现:要点是对于原数组的重排列,实现下标的正确排列

而这,正可以利用按位逆序置换来处理

整体详解
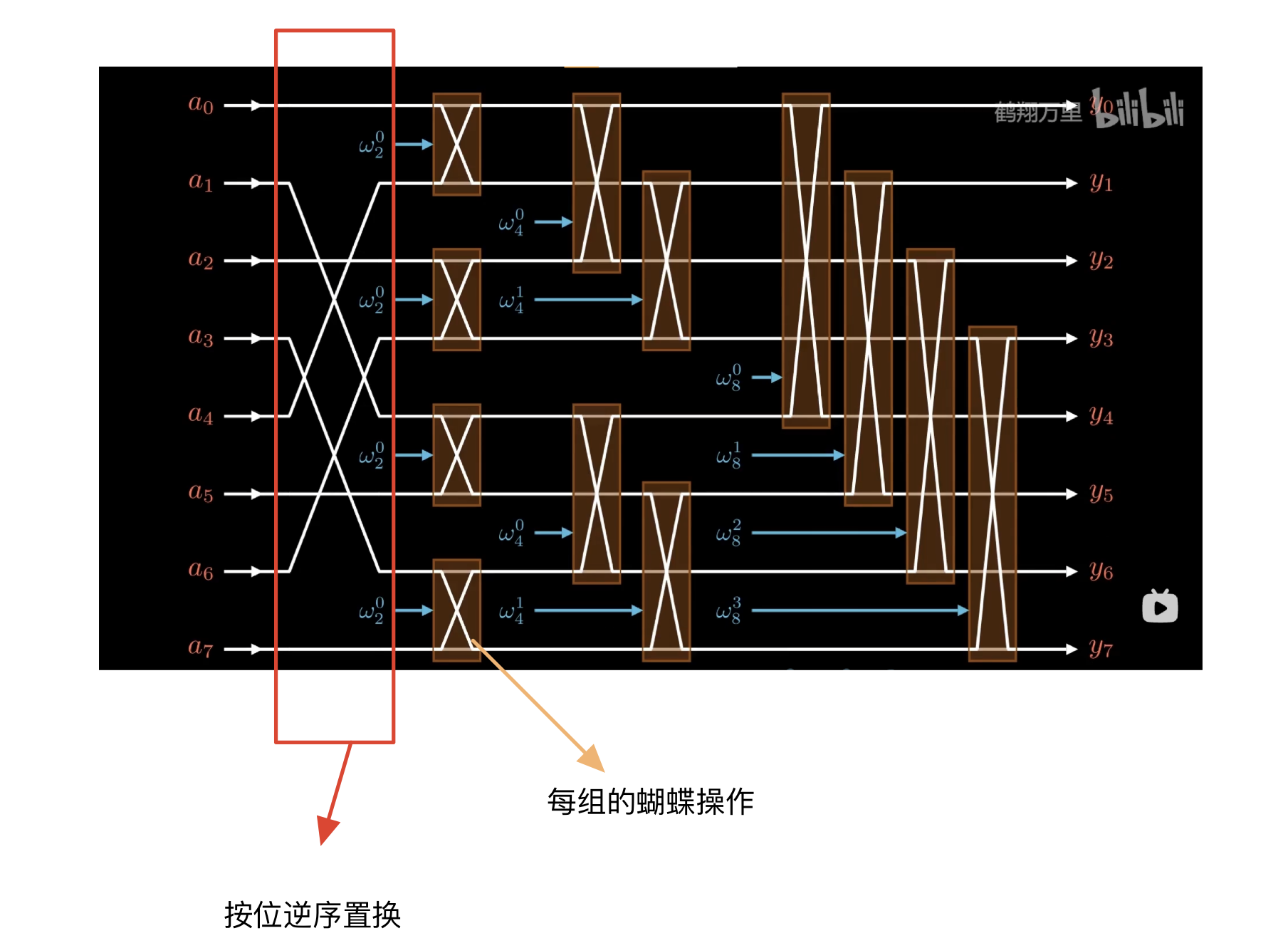
Matrix表示
这部分要是敲公式的话太多了,所以直接手写上图💺

补充 嗝~
IFFT
用傅里叶矩阵的逆(酉矩阵的性质)很容易就可以得出IFFT的表达式

ok,代码上其实只是改了一行

计算卷积(循环卷积)
方法很简单,就是先用FFT整成点值表示,然后点值乘法,再IFFT变成系数表示

结语 over
( •̀ ω •́ )y本人(咸鱼)的第一篇博客,以后的笔记会陆续上传
芜湖起飞!!!













